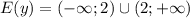Найти множество значений функции: y=cos 4x cos 3x + sin 4x sin 3x - 5 y=(sinx+cosx)^2 y=2x-1/x-2(в дан.случае кроме чисел :
Другие вопросы по теме Алгебра
Популярные вопросы
- Какой год шел перед 50 годом до н.э какой год был следующий после него...
1 - Увысокой муравьиной кучи ковром рассыпались знакомые лесные цветы. между...
1 - Определите к каким векам относятся 1800,1700,1900?...
2 - Запиши и прочти наибольшие десятизначное число,все цифры которого различные...
3 - Одно число больше другого на 0,62. найдите их сумму, если меньшее число 9,6...
3 - Окислительно-относительная реакция: kclo₃ + p = p₂o₅ + kcl...
3 - Два примера событий свидетелем которых ты был...
2 - Начертите отрезок кр и оа так, чтобы кр=5см3мм,оа=8см8мм...
3 - Почему вы считаете себя индивидуальностью? (характеристика)...
2 - Скажите сколько будет игрек разделить на 8 равно 3562...
2
Функция y = cosx изменяется в пределах от -1 до 1. Оценим в виде двойного неравенства
Множество значений функции![E(y)=[-6;-4]](/tpl/images/0075/1551/24d96.png)
Множество значений функции sin 2x - [-1;1]. Аналогично, оцениваем в виде двойного неравенства
Множество значений функции:![E(y)=[0;2].](/tpl/images/0075/1551/6a953.png)
Графиком функции является гипербола. Переходя к пределу при х стремящихся к бесконечности горизонтальная асимптота функции
Область значений функции :