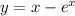Найти частное решение линейного однородного дифференциального уравнения.
Другие вопросы по теме Алгебра
Популярные вопросы
- 1319. Выполните действия:1) 9,8 .-3293) 4.3.• (-1/2) (-25185) -2,36 ·...
1 - ТВІР ІЗ ЗАРУБІЖНОЇ ЛІТЕРАТУРИ у пошуках себе і високого польоту за твором...
3 - Какое категория по степени ношения относится изделия туника?...
2 - Кому Анна Ахматова Посвятила своё стихотворение Художнику ?(мне все твоя...
2 - Ені зак3. Познач будову виділених прикметників.і за до яких суфіксів...
2 - Доску длиной 143, 88 см распилили на 2 части. одна часть больше другой...
2 - 2) Найдите значение выражения УМАЛЯЮ ...
2 - Из 100 лотерейных билетов в тридцати выигрыш состовляет 100 тыс. руб....
1 - Какой инструмент в Photoshop обладает теми же свойствами, что и маска?...
3 - План пригод мумі троля із казки Зима чарівниця...
2
Пусть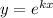 , получаем характеристическое уравнение
, получаем характеристическое уравнение
Общее решение линейного однородного диф. уравнения:
Подставив начальные условия, найдем константы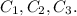
Частное решение: