1. Алгебра
  2. Найдите знаменатель прогрессии

Найдите знаменатель прогрессии xn, если x4= 2; x6= 1/2

миша1078 миша1078    3   18.05.2019 05:30    7

Ответы
kostyaborisenk3 kostyaborisenk3  30.09.2020 19:56

Известно, что каждый член геометрической прогрессии равен произведению предыдущего члена и знаменателя геометрической прогрессии (который обычно обозначается q, но пусть будет Xn).

x_{n} =x_{n-1}*Xn

Так как нам известны 4 и 6 члены прогрессии, нетрудно установить, что они отличаются в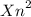 {Xn}^{2} раз:

x_{6}=x_{5}*Xn=x_{4}*Xn*Xn=x_{4}*{Xn}^{2}

Отсюда несложно найти Xn:

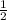
x_{4}*{Xn}^{2}=x_{6}\\ 2*{Xn}^{2}=\frac{1}{2}\\ {Xn}^{2}=\frac{1}{4}\\ {Xn}^{2}={(\frac{1}{2}) }^{2}

Xn=±\frac{1}{2}

ПОКАЗАТЬ ОТВЕТЫ
AliMsi AliMsi  30.09.2020 19:56

Используем формулу n-го члена геометрической прогрессии: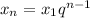 x_n=x_1q^{n-1}


x_6=x_1q^5=\underbrace{x_1q^3}_{x_4}\cdot q^2=x_4q^2~~\Leftrightarrow~~ q=\pm\sqrt{\dfrac{x_6}{x_4}}=\pm\sqrt{\dfrac{0.5}{2}}=\pm0.5



ответ: ± 0,5.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
LizaVasilenko3636 LizaVasilenko3636  14.12.2020 22:38
1/7 x²корень49x⁶ Упростите упражнение...
iiiiivvvv iiiiivvvv  14.12.2020 22:38
(x - 1)(x + 1)(x2+ 1) = 10x2– 10;​...
АннаЕжиха АннаЕжиха  14.12.2020 22:40
решить tg^3x+tg^2x -3tgx=3...
pirishok pirishok  14.12.2020 22:40
Найди сумму бесконечно убывающей геометрической прогрессии: а) 8 – 4 + 2 – 1 + 1/2 - 1/4 + …б) на фото​...
sock2 sock2  14.12.2020 22:42
Определи формулу линейной функции, график которой параллелен графику линейной функции 5x+2y+2=0 и проходит через точку M(2;2)....
Nzzjsjs Nzzjsjs  14.12.2020 22:43
В городе маленьком 15 телефонов. можно ли соединить их, так чтобы каждый был соеденён с пятью другими...
К18атя К18атя  14.12.2020 22:43
( ) Постройте график линейной функции у = -2х + 1. С графика найдите: а) значение у, если х = 3; б) значение х, если у = -1; в) значения переменной х, при которых значения...
DarkGay DarkGay  14.12.2020 22:43
Вычисление логарифмической производной решить задания...
двоишник55 двоишник55  14.12.2020 22:44
Найти сумму nпервых членов арифметической прогрессии, еслиa1 = 4, an = 63, n = 16. Найти сумму nпервых членов арифметической прогрессии: -0,7; -0,4; -0,1… n=7Найти сумму...
katakoval katakoval  14.12.2020 22:44
Назовите основные причины и предпосылки царских реформ. 2. Используя карту, покажите местонахождение окружных приказов и трех частей Младшего жуза. 3. Используя и связывая...

Популярные вопросы