Найдите значения выражения: 1) arccos(-cos 3pi/4); 2) cos(arcsin(-3/7))

Ответы

аввввввввввввввввввв 13.07.2020 08:06

Объяснение:

$1) arccos(-cos\frac{3\pi }{4} ) = arccos (- (-\frac{\sqrt{2} }{2} ))= arccos\frac{\sqrt{2} }{2} =\frac{\pi }{4} ;\\2) cos (arcsin(-\frac{3}{7} ))$

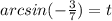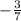Пусть $arcsin (-\frac{3}{7} ) = t$ ,Тогда sint = $-\frac{3}{7}$ ,

t - принадлежит четвертой четверти ( синус отрицательный ).

Значит теперь задание : найти cost при заданном значении синуса.

Воспользуемся основным тригонометрическим тождеством:

$sin^{2} t+cos^{2} t=1;\\cost= \sqrt{1-sin^{2} t} ;\\cost = \sqrt{1-(\frac{3}{7})^{2} }=\sqrt{1- \frac{9}{49} } =\sqrt{\frac{49}{49}-\frac{9}{49} }=\sqrt{\frac{40}{49} } =\frac{\sqrt{40} }{7} =\frac{2\sqrt{10} }{7} .$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

lui19 17.07.2019 01:10

Решить)) сейчас) найдите найбольшее значение функции y=log0,5(2+sinx) если можно с объяснением. большое))...

MihailoMK 17.07.2019 01:10

Постройте график функции y=-2 x +3 и найдите при каком значении x значение y=1,5...

denholopДанила23231 16.07.2019 22:21

1.серединный перпендикуляр-это прямая, проходящая через середину и: а) перпендикулярная к нему, б) разделяет данный отрезок пополам, в) равноудален от сторон угла. 2.сколько точек...

ЛизаНагайцева03 17.07.2019 01:10

Завтра нужно здать.а я не могу никак решить. точка а (m ; n), где m≠0, n≠0, принадлежит графику функции у=х². принадлежит ли графику функций точка: 1) b( m; -n). 2) c( -m; n)....

petrovakat2003 14.06.2019 09:10

Купили несколько роз по 70р. и несколько гвоздик по 50р.,заплатив за всю покупку 460р.сколько купили роз и сколько гвоздик?...

геймер39 14.06.2019 09:10

Кладчик поместил в банк 1227 р. банк ежегодно выплачивает вкладчику 4% от суммы вклада. какую сумму денег получит вкладчик через 2 года?...

эльвинчик2 14.06.2019 09:10

Решить при каких значениях m выражения 3m+7 и 5-7m принимают одно и то же значение? для каждого такого m найдите это значение...

Roblox777 14.06.2019 09:10

Функция задана формулой у=2х+7.найдите значение функции , соотвествующее значению аргумента , равному 1; -20; 43...

камран12 14.06.2019 09:10

Длина хорды окружности равна 96, а расстояние от центра окружности до этой хорды 20. найдите диаметр окружности....

llovich 14.06.2019 09:10

Даны векторы а(-3; 2) b(1; 6) найдите векторы a+b и a-b...

Найдите значения выражения: 1) arccos(-cos 3pi/4); 2) cos(arcsin(-3/7))

Популярные вопросы