1. Алгебра
  2. Найдите значение выражения

Найдите значение выражения т/пи,где т-главный период функции y=sin\frac{x}{3}

kirill20060729 kirill20060729    2   02.11.2019 15:38    0

Ответы
ruslankryoi ruslankryoi  11.09.2020 12:18

Известно, что у функции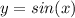 y=sin(x) главный период функции равен 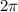2\pi. Что же будет с функцией, где аргумент в три раза меньше?

Например,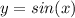 y=sin(x), максимума, то есть единицы, достигает при

$x=\frac{\pi}{2}, а у $y = sin\bigg (\frac{x}{3} \bigg), надо чтобы $ \frac{x}{3} = \frac{\pi }{2} \Rightarrow x=\frac{3\pi }{2}, то есть в три раза больше. То есть уменьшая аргумент, мы растягиваем функцию по оси ОХ. В данном случае растягиваем по ОХ в 3 раза. А значит, и период вырастет в три раза. Так как период sin(x) равен 2 \pi, то для нашей функции он будет равен 2\pi \cdot 3 = 6\pi

$T=6\pi; \frac{T}{\pi}=\frac{6 \pi}{\pi}=6

ответ: 6

P.S. для наглядности графики на картинке


Найдите значение выражения т/пи,где т-главный период функции y=sin<img src=" />
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Katerka Katerka  11.06.2019 22:10
Какое из уровнений не имеет корней 1) |у| -3=0. 3) х-7=-3 2) 1-z=3-2z. 4) 4-2s=5-2s...
prooverrseer prooverrseer  11.06.2019 22:10
(sin t-cos t)^2+2sin t cos t выражение...
NikikitaHyduak NikikitaHyduak  11.06.2019 22:10
Разность дробей а+2b/2c-а-4b/2c равна:...
alial1 alial1  11.08.2019 23:10
Среди чисел 0,6,9,13,35,37,38,49,72найдите корень уравнения: 1)х+14=23; 2)78+х=78 ; 3)х-16=22 ; 4)y-49=0; 5)24-y=11; 6)72-y=72....
Ele4ka17 Ele4ka17  11.08.2019 23:10
Розв яжіть рівняння икс в квадрате+икс=(икс+3)*(3 икс-2)-2...
catlolhd14 catlolhd14  11.08.2019 23:10
Найдите сумму всех трехзначных чисел, все цифры которых нечётные....
bayramovarzu bayramovarzu  28.11.2021 21:19
Яке з рівнянь не має розвязків а)х2=х6;б)х×х3=-1...
papashamuslimo papashamuslimo  28.11.2021 21:20
. Побудуйте графік функції у = х* – 8х + 12. Користуючись графіком, знайдіть: а) найменше значення функції; б) область значень функції;...
bahakendjaev11 bahakendjaev11  28.11.2021 21:20
найдите область определения для каждой функции...
arturka111 arturka111  28.11.2021 21:21
Можете памоч, пліз Бистреє...

Популярные вопросы