1. Алгебра
  2. Найдите значение следующего

Найдите значение следующего выражения, если tga=3 (sina+3cosa)/(sin^3a-3cos^3a)​

Liner158 Liner158    3   31.08.2020 20:41    1

Ответы
нэла1 нэла1  15.10.2020 16:31

tga=3\ \ \to \ \ \ \dfrac{sina}{cosa}=3\ \ ,\ \ sina=3cosa\ \ ,\\\\\\\dfrac{sina+3cosa}{sin^3a-3cos^3a}=\dfrac{3cosa+3cosa}{(3cosa)^3-3cos^3a}=\dfrac{6cosa}{27cos^3a-3cos^3a}=\dfrac{6cosa}{24cos^3a}=\\\\\\=\dfrac{6}{24\, cos^2a}=\dfrac{1}{4}\cdot \dfrac{1}{cos^2a}=\dfrac{1}{4}\cdot (1+tg^2a)=\dfrac{1}{4}\cdot (1+9)=\dfrac{10}{4}=\dfrac{5}{2}=2,5\\\\\\\boxed {\ 1+tg^2a=\dfrac{1}{cos^2a}\ }

ПОКАЗАТЬ ОТВЕТЫ
leravolk399 leravolk399  15.10.2020 16:31

(см. объяснение)

Объяснение:

Приведем исходную дробь к виду, в котором есть только тангенс альфа:

\dfrac{sina+3cosa}{sin^3a-3cos^3a}=\dfrac{tga\times (1+tg^2a)+3(1+tg^2a)}{tg^3a-3}=\dfrac{(1+tg^2a)(tga+3)}{tg^3a-3}

При tga=3:

\dfrac{(1+3^2)(3+3)}{3^3-3}=\dfrac{10\times6}{24}=\dfrac{5}{2}

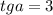Задание выполнено!

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
likeaboss2005 likeaboss2005  30.06.2019 06:30
1.на 15 га пашни посеяно 2,7 г пшеницы. сколько зерна потребуется для засева 1030 га пашни?...
bayan6 bayan6  30.06.2019 06:30
За одного человека проголосовала 75%. за второго 10%, 30 бюллетени недействительны. сколько проголосовало...
ммммм89 ммммм89  30.06.2019 06:30
Решите : мастерская планировала сшить партию юбок для танцевального ансамбля за 12 дней.однако ежедневно удалось шить на 1 юбку больше,чем планировалось ранее,и...
lilililiza lilililiza  30.06.2019 06:30
30 . разложить многочлен на множители. 15b^3 - 3 (вынесение общего множителя за скобки и по формулам) 4c^2+6c+4+6c...
kholmatova002 kholmatova002  30.06.2019 06:30
Разложите на множители: а) 2х^2•у+4ху^2...
ViolettAHS ViolettAHS  30.06.2019 06:30
20 . расписать выражение оч. надо . √(12) + √(12)= 20 ....
Asylai5A Asylai5A  30.06.2019 06:30
Решите систему уравнений 2х+у=3 х-3у=5...
maninigorek maninigorek  30.06.2019 06:30
1.разложите на множители выражение 3х^6-27х^2y^2. 2.решите уравнение 2х-5/4-6х+1/8=2. 3.найдите значение выражения -3*(2/3)^2-0.5^2 решите , от этой контрольной...
LitRoboBoytle LitRoboBoytle  13.05.2020 12:20
УМОЛЯЮ Путешественник разбил маршрут на 2 части. Первые x км онпреодолевает за 3 часа, а следующие у км за 2 часа.С какой средней скоростью двигался путешественник?Впишите...
Skillet121516 Skillet121516  13.05.2020 12:26
2 x (x4-5x + 3) представте в виде многочлена​...

Популярные вопросы