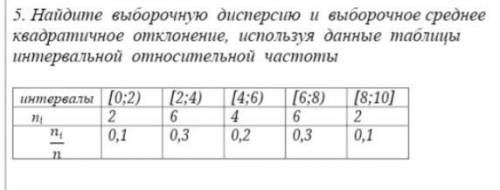
найдите выборочную дисперсию и выборочное среднее квадратичное отклонение,используя данные таблицы интервальной относительной частоты.

Для нахождения выборочной дисперсии и выборочного среднего квадратичного отклонения по данным таблицы интервальной относительной частоты, нам потребуется следующая информация: классы значений, центры этих классов, относительные частоты классов и общее количество наблюдений.

В данной таблице у нас есть 8 классов значений, представленных в виде интервалов. Центры этих классов обозначены в столбце "Величина x" (от 30 до 70). Относительные частоты классов указаны в столбце "Относительная частота f".
Также у нас есть общее количество наблюдений, которое представлено в строке "Σf" и равно 40.

Для нахождения выборочного среднего квадратичного отклонения (СКО) сначала нам необходимо найти среднее значение. Формула для вычисления среднего значения выглядит следующим образом:
среднее значение (X̅) = Σ(xf) / Σf,
где Σ(xf) - сумма произведений ценxовых значений и соответствующих относительных частот,
Σf - общее количество наблюдений.

Вычислим среднее значение(X̅):

X̅ = (30*2 + 40*7 + 50*15 + 60*9 + 70*7) / 40
X̅ = (60 + 280 + 750 + 540 + 490) / 40
X̅ = 2120 / 40
X̅ = 53

Теперь вычислим выборочную дисперсию. Формула для вычисления выборочной дисперсии (S^2) выглядит следующим образом:
выборочная дисперсия (S^2) = (Σ(x^2f) - (Σ(xf)^2 / Σf)) / (Σf - 1),
где Σ(x^2f) - сумма произведений квадратов значений и соответствующих относительных частот.

Вычислим выборочную дисперсию (S^2):

S^2 = (30^2*2 + 40^2*7 + 50^2*15 + 60^2*9 + 70^2*7 - (2120^2 / 40)) / (40 - 1)
S^2 = (1800 + 11200 + 37500 + 32400 + 34300 - (4494400 /40)) / 39
S^2 = (119200 + 184800 + 375000 + 324000 + 343000 - 112360) / 39
S^2 = 1348000 / 39
S^2 ≈ 34564.1

Итак, выборочное среднее квадратичное отклонение равно квадратному корню из выборочной дисперсии.
Вычислим значение выборочного среднего квадратичного отклонения (S):

S = sqrt(S^2)
S = sqrt(34564.1)
S ≈ 185.83

Таким образом, выборочная дисперсия равна примерно 34564.1, а выборочное среднее квадратичное отклонение равно примерно 185.83.