Найдите все значения параметра a,при котором у уравнения есть одно решение

ответ: при a ∈ (-7/4; 1/2].

Объяснение:

Пусть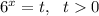 , тогда получаем уравнение

                               (*)

D = (8a+5)² - 4(16a² + 20a - 14) = 64a² + 80a + 25 - 64a² - 80a+56 = 81

Используем теорему Виета

x₁ + x₂ = 8a + 5

x₁x₂ = 16a² + 20a - 14

Исходное уравнение имеет одно решение, если корни квадратного уравнения (*) имеют разные знаки. Это возможно, когда :

16a² + 20a - 14 < 0

8a² + 10a - 7 < 0

(4a + 7) * (4a-2) < 0

+++++++++(-7/4)------------(1/2)+++++++++++

Но, если подставить a=1/2, получим одно решение.

При a ∈ (-7/4; 1/2] уравнение имеет одно решение.

Замена

Чтобы исходное уравнение имело один корень, нужно чтобы получившееся после замены квадратной кравнение имело один полодительный и один неположительный корень, то есть, чтобы