Найдите все значения параметра а, при каждом из которых уравнение 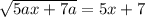
Другие вопросы по теме Алгебра
Популярные вопросы
- АD=40см,AB=17см,CD==8см.Найди:a)BC.b) Расстояние между серединами отрезков...
1 - Задание 2. Заполните таблицу: охарактеризуйте внутреннее положение и внешнюю...
1 - Скласти речення з словом On the other hand тема шопінг...
1 - Ещё вопрос как решить (6,8-4,7):1 2/5...
2 - Обчислити похідну функції: у = х∙sinх...
2 - с физикой Каково значение ЭДС в проводнике, когда он находится между полюсами?...
3 - Привет Нужно выписать все действительные причастия настоящего времени и обозначить...
3 - Хімія 10 клас практична 5чень надо...
1 - Потрібно написати з англ мови 12 реч. зі словом 1 He is smaller than I2 We...
3 - Чи правильно виконане множення? ( - 2х2у + 3ху - х2) · ху2 = - 2х3у3 + 3х2у3...
2
1. Возведем оба выражения уравнения в квадрат, чтобы устранить корень:
(√(5ax + 7a))^2 = (5x + 7)^2
5ax + 7a = (5x + 7)^2
2. Упростим квадрат справа:
5ax + 7a = 25x^2 + 70x + 49
3. Перенесем все выражения на одну сторону уравнения:
25x^2 + (70 - 5a)x + (49 - 7a) = 0
4. Для того чтобы это квадратное уравнение имело решение, его дискриминант должен быть больше или равен нулю:
D = (70 - 5a)^2 - 4 * 25 * (49 - 7a) ≥ 0
Раскрываем скобки и сокращаем подобные слагаемые:
25a^2 - 490a + 2401 - 700a + 980 ≥ 0
25a^2 - 1190a + 3381 ≥ 0
5. Теперь мы можем решить неравенство, найдя значения параметра a, удовлетворяющие неравенству:
Поскольку у нас квадратное уравнение, мы знаем, что апараходы ветвей параболы будут выше или ниже оси абсцисс в зависимости от знака коэффициента при a^2. Таким образом, у нас есть два случая:
1) Уравнение имеет решение, если дискриминант равен нулю:
D = 0
25a^2 - 1190a + 3381 = 0
Для решения этого квадратного уравнения можно использовать формулу дискриминанта и получить значения параметра a.
2) Уравнение имеет решение, если дискриминант больше нуля:
D > 0
25a^2 - 1190a + 3381 > 0
Можно использовать метод интервалов для решения этого неравенства и определить интервалы, в которых должен находиться параметр a.
Таким образом, значения параметра a, при которых уравнение имеет решение, можно найти, решив квадратное уравнение при D = 0 и использовать метод интервалов для квадратного уравнения при D > 0.