Найдите угол, который образует с положительным лучом оси абсцисс касательная к графику функции y = x^8/8 - x^5/5 - x√3 - 3 в точке x(нулевое) = 1
Ответы
Тангенс угла наклона касательнойв точке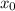 к положительному направлению оси х равен значению производной этой функции в точке
к положительному направлению оси х равен значению производной этой функции в точке 
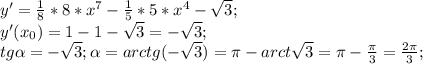 Или 120 градусов
Или 120 градусов
ПОКАЗАТЬ ОТВЕТЫ
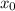 к положительному направлению оси х равен значению производной этой функции в точке
к положительному направлению оси х равен значению производной этой функции в точке 
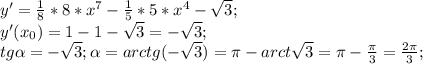 Или 120 градусов
Или 120 градусов
Другие вопросы по теме Алгебра
Популярные вопросы
- Много только 1 , 4 , 6 надо либо любой из этих трех и побыстрее...
3 - Можете примеры на интернациональную лексику...
3 - Решить 3 (в виде блок схем,желательно на листке)...
1 - Выбери правильный ответ.углеводороды с одинарными связями в молекуле:...
1 - Кусок сплава из свинца и олова массой 400 гр имеет плотность 8,3 г/см (куб)....
3 - Вправа по тексту! подробности на фото вашей...
2 - Какое число надо вписать в окошко, чтобы равенство 8=56/пусто стало верным...
3 - Скиньте самые необходимые слова языка...
3 - Чел и свет мая радима беларусь 2018 г издания параграф 28 намаляваць герб...
2 - Как ты думаешь, жираф знал, что вулкан взорвётся так вкусно и красиво? итоговая...
1