Найдите точки максимума и минимума функции f(x)=5-4x-4x^2
Другие вопросы по теме Алгебра
Популярные вопросы
- Расскажите о своем рабочем дне, используя следующие речевые образцы. My...
3 - Помните с заданием, это СОЧ по математике 6 класс...
3 - Найдите фокальные радиусы эллипса симметричного относительно осей координат,...
3 - 1) Сколько минимум миллиардов лейкоцитов содержит в норме 1 литр крови?...
1 - Приветики мои друзья. Давайте поболтаем. Но не с мальчиком. Я девочка....
3 - 7. При реакции соединения: A) в реакцию вступают два сложных вещества, при...
3 - Их сравним. +—«Компьютерная» технология:«Бумажная» технология:+ удобство...
2 - 6. Наибольшая массовая доля азота содержится в A) NO2 B) N2O4 C) NO D) N2O5...
2 - Переведите фразу на английский без переводчика Я создана только для тех,...
1 - Вычислите площадь кругового сектора радиуса R= 6e+0см, ограниченного дугой...
2
Данная функция - квадратичная (функция, уравнение которой включает в себя переменную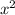 ). Стандартный вид функции:
). Стандартный вид функции:  .
.
То есть в нашей функции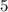 это
это  ,
, 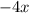 это
это  и
и 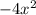 это
это 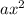 .
.
Стандартный вид функции:График квадратичной функции - парабола (геометрическое место точек, равноудалённых от данной прямой). Ветви параболы могут быть направлены вверх и вниз.
Если коэффициент при переменной
при переменной 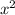 положительный, то ветви параболы направлены вверх. Если же коэффициент отрицательный, то ветви параболы направлены вниз.
положительный, то ветви параболы направлены вверх. Если же коэффициент отрицательный, то ветви параболы направлены вниз.
Координата вершины параболы - значение
вершины параболы - значение  . Если квадратичная функция записана в стандартном виде
. Если квадратичная функция записана в стандартном виде 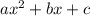 , воспользуемся коэффициентами
, воспользуемся коэффициентами  и
и 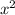 :
:
В функцииМы ищем максимум функции, так как ветви параболы направлены вниз. Чтобы найти максимум нужно подставить в исходную функцию найденное значение
найденное значение  .
.
Точка максимума функции равна .
.