Найдите точки экстремумы функции
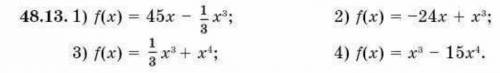
Другие вопросы по теме Алгебра
Популярные вопросы
- Линейное уравнение с одной переменной, переменная которого задана...
3 - Розписати 13 і 18 елемент з хімії...
2 - Известно, что ген гемофилии (несвертываемость крови) — рецессивный...
1 - Where did Asadbek study comming to Tashkent...
2 - ответьте на вопросы ЕСЛИ НЕ ЗНАЕТЕ ОТВЕТ ТО НЕ ПИШИТЕ ПОТОМУ ЧТО...
3 - Найти корни уравнения принадлежащие промежутку (0;2п)...
2 - С Напишем программу, которая имитирует процесс ввода пароля: если...
3 - (9-5)÷2+(8+3)×5-(8-4)×6+7×9+11-3+6×(3-0)=...
1 - Представьте число 2 456 в виде суммы: 1) двух четырехзначных чисел;...
1 - Что такое развёрнутый и сжатый аргумент а русском языке?...
2
- + -
_____- 3√5______ 3√5 _____
min max
x = - 3√5 - точка минимума, так как при переходе через эту точку призводная меняет знак с "-" на "+" .
x = 3√5 - точка максимума, так как при переходе через эту точку призводная меняет знак с "+" на "-" .
2) f(x) = - 24x + x³
f'(x) = - 24(x)' + (x³)' = - 24 + 3x²
f'(x) = 0 ⇒ - 24 + 3x² = 0
x² = 8
x₁,₂ = ± √8 = ± 2√2
+ - +
______ - 2√2 ______ 2√2 ______
max min
- + +
______ - 0,25 ____________0_____
min точка перегиба
4) f(x) = x³ - 15x⁴
f'(x) = (x³)' - 15(x⁴)'= 3x² - 15 * 4x³ = 3x² - 60x³ = 3x²(1 - 20x)
f'(x) = 0
3x² (1 - 20x) = 0
x₁ = 0
x₂ = 0,05
+ + -
______ 0,05 _______ 0 ______
точка перегиба max