Найдите те значения аргумента, при которых значения производной функции 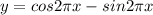 равны
равны 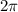 . В ответе запишите наименьшее положительное значение аргумента.
. В ответе запишите наименьшее положительное значение аргумента.
Другие вопросы по теме Алгебра
Популярные вопросы
- 4. Разность двух углов, образовавшихся при пересечении двух прямых, равна 42° Найдите...
3 - Памагите п.ж вам55 звёздочек и 55 лаиков памагите п.ж...
3 - 3. Прочитайте витяг із статті та визначте причини сирітства, з’ясуйте інші причини...
3 - 15. Значение слова «теле» А) УйгурВ) КарлукС) ТюркD) ОгузЕ) Кимак ОЛИМПИАДА ...
2 - Сколько натуральных чисел находится между числами 22 и 33 ...
2 - Чем является в предложении «Ярко светит солнце» слово ярко? a. обстоятельство b....
1 - Прилагательные и существительные с приставкой с и з какие есть...
3 - Среди описанных ситуаций выбери примеры диффузии. Большой резиновый шар, наполненный...
3 - Используя тектоническу карту атласа стр. 12-13 и геохронологическую таблицу на стр....
3 - создать хронику Тройственного союза и Антанты...
1
Шаг 1: Найдем производную функции y по аргументу x с помощью правила дифференцирования сложной функции:
y' = d/dx(cos^2(πx) - sin^2(πx))
Для этого воспользуемся формулой для производной функции cos^2(u) и sin^2(u):
y' = d/dx(cos^2(πx)) - d/dx(sin^2(πx))
Здесь u = πx.
Применяя правило дифференцирования, получим:
y' = 2cos(πx)(-sin(πx)π) - 2sin(πx)(-cos(πx)π)
Здесь мы использовали правило производной сложной функции.
Таким образом, мы получаем производную функции y равной:
y' = -2πsin(πx)cos(πx) - 2πcos(πx)sin(πx)
Шаг 2: Теперь приравняем полученное значение производной к значению 2π и найдем значения аргумента x:
-2πsin(πx)cos(πx) - 2πcos(πx)sin(πx) = 2π
Упрощаем выражение, убирая общий множитель 2π:
-sin(πx)cos(πx) - cos(πx)sin(πx) = 1
Исключаем синусы и косинусы, замечая, что последние суммируются в нуль:
-2sin(πx)cos(πx) = 1
Делим обе части на -2:
sin(πx)cos(πx) = -1/2
Шаг 3: Ищем значения аргумента, при которых sin(πx)cos(πx) равно -1/2. Заметим, что sin(πx) и cos(πx) принимают значения -1, 0 и 1.
Приравниваем sin(πx) и cos(πx) к значениям:
sin(πx) = 1, cos(πx) = -1/2
sin(πx) = -1, cos(πx) = 1/2
sin(πx) = 1/2, cos(πx) = -1
sin(πx) = -1/2, cos(πx) = 1
Следовательно, мы получаем 4 уравнения:
1) sin(πx) = 1, cos(πx) = -1/2
2) sin(πx) = -1, cos(πx) = 1/2
3) sin(πx) = 1/2, cos(πx) = -1
4) sin(πx) = -1/2, cos(πx) = 1
Шаг 4: Решаем каждое из уравнений.
1) sin(πx) = 1, cos(πx) = -1/2
Заметим, что sin(πx) не может быть равным 1 при любом значении x, так как sin(πx) принимает значения только от -1 до 1.
Поэтому это уравнение не имеет решений.
2) sin(πx) = -1, cos(πx) = 1/2
Заметим, что sin(πx) не может быть равным -1 при любом значении x, так как sin(πx) принимает значения только от -1 до 1.
Поэтому это уравнение не имеет решений.
3) sin(πx) = 1/2, cos(πx) = -1
Заметим, что sin(πx) равен 1/2 при x = 1/6, так как sin(π/6) = 1/2, а cos(πx) равен -1 при x = 1/2, так как cos(π/2) = -1.
Поэтому этому уравнению соответствует решение x = 1/6.
4) sin(πx) = -1/2, cos(πx) = 1
Заметим, что sin(πx) равен -1/2 при x = 5/6, так как sin(5π/6) = -1/2, а cos(πx) равен 1 при x = 0, так как cos(0) = 1.
Поэтому этому уравнению соответствует решение x = 5/6.
Шаг 5: Найдем наименьшее положительное значение аргумента, которое является решением уравнений.
x = 1/6 и x = 5/6 являются решениями нашей задачи. Нам необходимо выбрать наименьшее положительное значение, которое соответствует этим решениям.
Сравниваем значения x = 1/6 и x = 5/6 и видим, что наименьшее положительное значение аргумента равно 1/6.
Ответ: Наименьшее положительное значение аргумента равно 1/6.