Найдите те решения уравнения, для которых определено выржаение g(x):

sin6x*cos6x=cos( $\frac{\pi }{2}$ -4x), g(x)=tg (4x+ $\frac{\pi }{2}$ )

Ответы

maks2614 04.10.2020 13:55

В левой части уравнения применим формулу синуса двойного угла, а в правой части по формуле приведения

$0.5\sin 12x=\sin 4x\\ \\ \sin 12x=2\sin4x\\ \\ \sin 12x-\sin 4x-\sin 4x=0\\ \\ 2\sin\dfrac{12x-4x}{2}\cos\dfrac{12x+4x}{2}-\sin 4x=0\\ \\ 2\sin4x\cos8x-\sin 4x=0\\ \\ \sin4x(2\cos 8x-1)=0$

Произведение равно нулю в том случае, когда хотя бы один из множителей обращается к нулю

$\sin 4x=0$

$2\cos 8x-1=0\\ \\ \cos 8x=\dfrac{1}{2}\\ \\ 1-2\sin^24x=\dfrac{1}{2}\\ \\ \sin^24x=\dfrac{1}{4}$

далее воспользуемся тождеством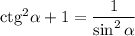 ${\rm ctg}^2 \alpha+1=\dfrac{1}{\sin^2\alpha}$ , получим

${\rm ctg}^24x+1=4\\ \\ {\rm ctg}^24x=3\\ \\ {\rm tg}^2\left(4x+\frac{\pi}{2}\right)=3\\ \\ {\rm tg}\left(4x+\frac{\pi}{2}\right)=\pm\sqrt{3}$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

mariaks16 06.04.2021 18:30

Задать формулой Линейную функцию график который Проходит параллельно прямой у=-8х+9 И пересекает ось ординат в точке (0; -1)...

MiraQeen 06.04.2021 18:30

У кого есть такая книга? нужна страница 210-211...

Zggzsbsnnzh 06.04.2021 18:30

Ребят решите это, до сегодня надо сдать а я не ебу что это)))...

DIMAES0 06.04.2021 18:31

1. Тест из 5 вопросов  1. Найдите значение алгебраической дроби 3х4, при х=1 а) 0,75 б) -0,75 в) 1 г) -1,52. Какое из предложенных выражений записано в виде алгебраическойдроби?а)...

SensRow 06.04.2021 18:31

Найти уравнение касательной к графику функции f(x)=x^2-4x-10, которая параллельна прямой y= -6x-7....

pointbreakk9 06.04.2021 18:31

, нужно до 07:04:2021 :) ...

YuliaPyatova 06.04.2021 18:33

5. Решите неравенство:а) – 6x 42; б) 15x - 24 -х+4....

zheniskanovaa 22.09.2019 01:50

4sin x умножить cos x sin(a+b)-cos a sin b...

20jeka 22.09.2019 01:50

2cos квадрат альфа-1 tg 3x-tg 2x/1+tg2x умножить tg 3x...

12355689 27.05.2020 16:33

Яка з наведених послідовностей є арифметичною прогресією А) 3; 6; 12; 24;... Б) 7; 10; 12; 13; B) -10; 0; 10; -10;... Г) 20; 17; 14; 11;......

Найдите те решения уравнения, для которых определено выржаение g(x): sin6x*cos6x=cos( -4x), g(x)=tg (4x+ )

Популярные вопросы

Найдите те решения уравнения, для которых определено выржаение g(x):

sin6x*cos6x=cos( $\frac{\pi }{2}$ -4x), g(x)=tg (4x+ $\frac{\pi }{2}$ )