Найдите сумму всех натуральных чисел, кратных 3 и не превосходящих 100.

Question

Алгебра: Найдите сумму всех натуральных чисел, кратных 3 и не превосходящих 100.

Ariana20199 · Answer

Данные числа являются арифметической прогрессией, где а₁=3; а₃₃=99. Соответственно d=3.((99-3)/32).

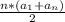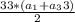Сумма членов арифметической прогрессии равна $\frac{n*(a_1+a_n)}{2}$ . В данном случае $\frac{33*(a_1+a_33)}{2}$ .

Значит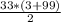 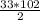$\frac{33*(3+99)}{2}$ = $\frac{33*102}{2}$ = 1683.

ответ: 1683.