1. Алгебра
  2. Найдите сумму всех целых

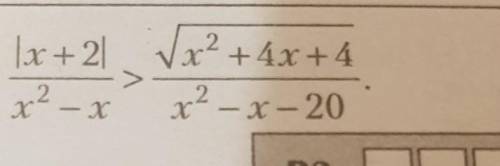
Найдите сумму всех целых решений неравенства (решение)​


Найдите сумму всех целых решений неравенства (решение)​

savitar228 savitar228    2   15.06.2021 02:36    1

Ответы
Рикашикина Рикашикина  15.07.2021 03:19

5

Объяснение:

\displaystyle\\\frac{|x+2|}{x^2-x} \frac{\sqrt{x^2+4x+4} }{x^2-x-20} \\\\\\\frac{|x+2|}{x^2-x} \frac{\sqrt{(x+2)^2} }{x^2-x-20} \\\\\\\frac{|x+2|}{x^2-x} \frac{|x+2|}{x^2-x-20}\\\\\\ \frac{|x+2|}{x^2-x} -\frac{|x+2|}{x^2-x-20}0\\\\\\|x+2|*\Big(\frac{1}{x^2-x} -\frac{1}{x^2-x-20}\Big) 0\\\\\\|x+2|*\frac{x^2-x-20-x^2+x}{x(x-1)(x+4)(x-5)}0 \\\\\\|x+2|*\frac{20}{x(x-1)(x+4)(x-5)}

|x + 2| ≥0 ,  но у нас строгое неравенство,

значит из решений надо исключить х= - 2

рассмотрим второй множитель

решим методом интервалов

нули : -4; 0; 1; 5

+++(-4)---(0)+++(1)---(5)+++>x

x ∈ (-4; 0) ∪ (1; 5)

исключим х = - 2

решением неравенства является

x ∈ (-4; -2) ∪(-2; 0) ∪ (1; 5)

найдем  сумму всех целых решений неравенства

-3 + (-1) + 0 + 2 + 3 + 4 = 5

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Mazadinec Mazadinec  09.04.2020 20:16
Реши систему уравнений: {3y+2x=6 {2x−2y=0 Х=? У=?...
roldugina78 roldugina78  09.04.2020 20:16
1) На рисунке изображен график функции y=f(x) на отрезке [-3;3]. Найдите f(-1) (в ответ напишите только число) https://imgur.com/a/dGBA8fI 2) На рисунке изображен график функции...
Кимчи12 Кимчи12  09.04.2020 20:17
Визнач значення т, при якому розв язком рівняння т. +4y - 12m=0 є парачисел (22;12,5).​...
olgakorneva1 olgakorneva1  09.04.2020 20:17
ОЧЕНЬ ОЧЕНЬ 1. Найти координаты вершины параболы: 1) у= 5х2+ 3х 2) у= х2+ 8х+ 16 3) у= - 3х2+ 18х+ 7 2. Выяснить, через какую точку оси абсцисс проходит ось симметрии параболы:...
Amarov Amarov  09.04.2020 20:17
Найди корни квадратного уравнения x2+4x+4=0...
няхамилаха няхамилаха  09.04.2020 20:17
Коренем якого з поданих рівнянь є число 2? ( с ришением А) 8х=4 Б)-3х=6 В)2х=2х+2 Г)7х+5=19...
Anazrk Anazrk  09.04.2020 20:17
Разложите на множители а)4х2у2-9а4= б)25а2-(а+3)2= в)27m3+n3=...
1234567891248 1234567891248  03.12.2020 15:15
Найдите область определения функции y=x+15x 1.D(y): x - любое число 2.D(y): x≠5 3.D(y): x≠0 и x≠−1 4.D(y): x≠−1 5.D(y): x≠0...
NaumYT NaumYT  03.12.2020 15:15
Решите извеняюсь за кривоту)​...
andreyoy andreyoy  03.12.2020 15:15
При каком значении x значение выражения 2x−1/x+18 равно 4?...

Популярные вопросы