1. Алгебра
  2. Найдите сумму шестнадцати первых

Найдите сумму шестнадцати первых членов арифметической прогрессии (аn), если а3=115, а14=65.

Артерия Артерия    2   16.09.2019 17:00    1

Ответы
Женя220V Женя220V  07.10.2020 20:08

Используем формулу n-го члена арифметической прогрессии:

                                    a_n=a_1+(n-1)d

a_{14}=a_1+13d=\underbrace{a_1+2d}_{a_3}+11d=a_3+11d\\ \\ d=\dfrac{a_{14}-a_3}{11}=\dfrac{65-115}{11}=-\dfrac{50}{11}


Первый член: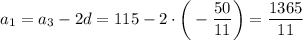 a_1=a_3-2d=115-2\cdot\bigg(-\dfrac{50}{11}\bigg)=\dfrac{1365}{11}



Осталось найти сумму шестнадцати первых членов арифметической прогрессии

S_{16}=\dfrac{2a_1+15d}{2}\cdot16=8\cdot\bigg(2\cdot\dfrac{1365}{11}+15\cdot\bigg(-\dfrac{50}{11}\bigg)\bigg)=1440



ответ: 1440.

ПОКАЗАТЬ ОТВЕТЫ
aksinaa9 aksinaa9  07.10.2020 20:08

                            Решение :  //////////////////////////////////


Найдите сумму шестнадцати первых членов арифметической прогрессии (аn), если а3=115, а14=65.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Анкта Анкта  26.05.2020 10:27
Дана функция y=f(x), где f(x)={−3x,если x 0 -x^2 если.x 0 вычислить...
SEMKA22444 SEMKA22444  26.05.2020 10:27
. У Люды стоят следующие оценки по алгебре: 2, 3, 2, 4, 2, 3. Какое из следующих утверждений представляется справедливым: а) частота получения двойки Людой за этот период...
llllloolllllllllk llllloolllllllllk  26.05.2020 10:27
Одне чисто вдвічі більше другого, а їхня сума дорівнює 24 Алгебра, система рівнянь...
Lizankanahovicyn Lizankanahovicyn  26.05.2020 10:22
2. У выражение: 2√27 + 5√75 – 1/4√48 - 14√3...
paolo99 paolo99  26.05.2020 10:06
решить ОБЯЗАТЕЛЬНО С РЕШЕНИЕМ решить ОБЯЗАТЕЛЬНО С РЕШЕНИЕМ >...
mgurbo mgurbo  26.05.2020 10:06
За 7 кг картоплі і 4 кг моркви заплатили 26 грн. скільки коштує 1 кг картоплі і 1 кг моркви, якщо 5кг картоплі дорожче 2 кг моркви на 4 грн?...
liza13100 liza13100  25.08.2019 15:10
Выражение: (cos^2a+2sinacosa-sin^2a)^2...
serega7315 serega7315  25.08.2019 15:10
Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в два раза? как решить?...
MihailoMK MihailoMK  25.08.2019 15:10
Одновременно подбросили три монеты. какова вероятность того, что ровно на двух из этих монет выпадет герб?...
muliku muliku  25.08.2019 15:10
Найдите сумму бесконечной прогрессии,если в1=6,q= -1/3 найдите первый член бесконечной прогрессии,если q -3/4 и s=8...

Популярные вопросы