1. Алгебра
  2. Найдите сумму решений

Найдите сумму решений уравнения tg2x * cos2x = sin2x + sin4x, принадлежащих множеству [-п; 2п]

Настасья020704 Настасья020704    3   08.03.2019 03:50    2

Ответы
BOILHbIU BOILHbIU  24.05.2020 04:50

Перепишем уравнение, учитывая, что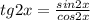 tg2x=\frac{sin2x}{cos2x}

\frac{sin2x}{cos2x}*cos2x=sin2x+sin4x -----(1)

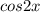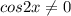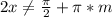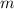В уравнение (1) выражение cos2x находится в знаменателе, поэтому cos2x\neq0, или  2x\neq\frac{\pi}{2}+\pi*m, m - целое

или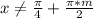  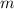x\neq\frac{\pi}{4}+\frac{\pi*m}{2}, m - целое-----(2)

Сократим в левой части уравнения (1) на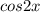 cos2x:

  sin2x=sin2x+sin4x, отсюда sin4x=0, отсюда

  4x=\pi*n, или x=\frac{\pi*n}{4}, n - целое ------(3)

Из решений (3) надо исключить значения, равные значениям (2):

 x=\frac{\pi*n}{4}\neq\frac{\pi}{4}+\frac{\pi*m}{2}, отсюда

  \pi*n\neq\pi+2\pi*m, сокращая на \pi, получим

  n\neq1+2*m - нечетные числа 

Другими словами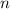 n принимает только четные значения!

 Из условия следует, что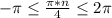 -\pi \leq\frac{\pi*n}{4}\leq2\pi, отсюда

    -4 \leq\ n \leq 8

Таким образом,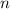 n принимает значения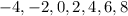 {-4, -2, 0, 2, 4, 6, 8}

Видно, что решения (3) уравнения составляют арифметическую прогрессию с первым членом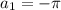 a_{1}=-\pi и последним седьмым членом

 a_{7}=\frac{8*\pi}{4}=2\pi 

Теперь мы можем найти сумму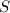 S всех решений уравнения как сумму первых семи членов арифметической прогрессии: 

S=7*\frac{a_{1}+a_{7}}{2}=7*\frac{-\pi+2\pi}{2}=3,5*\pi

 

 

 

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
liza1433 liza1433  15.05.2020 10:18
Знайдіть множину розв язків системи x-4 3...
sirius830 sirius830  15.05.2020 10:18
Х1=2пн, н€z X2=+/-arccos1/6+2пк, k€z...
EvelEvg EvelEvg  15.05.2020 10:18
Вариант 2 1. Выразит переменную у из уравнений: а) х - у = 3; б) 3х + 2у = 7 2. Решите методом подстановки систему уравнений 3x-y=1 5x-3y=11 3. Решите методом сложения систему...
derest derest  15.05.2020 10:18
Часы со стрелками показывают 1 час 30 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?​...
Mehriban2007 Mehriban2007  07.10.2019 00:10
203 в кадрате - 406 * 103 + 103 в квадрате ❤❤ по свойствам, без огромных чисел нужно...
andrekunshin andrekunshin  07.10.2019 00:10
Предсьавьте многочлен в виде произвкдения ав-ас-вх+сх+с-6...
cook16 cook16  07.10.2019 00:10
Выполните действия: а) (3 + t)2 б) (а – 7с)2 в) 3(t – п)2 +4tп!...
11martandreyp0bwg2 11martandreyp0bwg2  06.10.2019 23:05
когда автомобиль проехал часть пути от а до в , оказалось , что он проехал столько километров, сколько минут ему прийдется ехать часть пути ,которая осталась.но , когда он...
Lososepotam Lososepotam  07.10.2019 00:10
[tex]f(x) * f (x)\leq 0\\f(x)=x^2-2x-3[/tex]...
Tam192837465 Tam192837465  06.06.2019 12:10
Решите систему линейного уравнения сложения решите системы линейных уравнений сложения: б) 4х-3у=3, 4х-7у=-5. (система)...

Популярные вопросы