Найдите сумму n первых членов геометрической прогрессии, когда b1=2, q=-3

Сумма n первых членов геометрической прогрессии вычисляется по формуле  .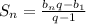

Конечно, я помогу вам решить эту задачу!

Итак, у нас есть геометрическая прогрессия, где первый член равен 2 (b1 = 2) и знаменатель равен -3 (q = -3). Мы должны найти сумму первых n членов этой прогрессии.

Для решения этой задачи существует формула для суммы n первых членов геометрической прогрессии:

Sn = b1 * (1 - q^n) / (1 - q)

Где Sn - сумма n первых членов прогрессии, q - знаменатель, а b1 - первый член прогрессии.

Теперь, чтобы применить формулу, нам нужно знать значения b1 и q. В нашем случае b1 = 2 и q = -3, поэтому мы можем заменить их в формуле:

Sn = 2 * (1 - (-3)^n) / (1 - (-3))

Теперь давайте приступим к пошаговому решению примера:

1. Первым шагом, вам нужно взять величину n, то есть количество членов, сумму которых вы хотите найти. Допустим, мы хотим найти сумму первых 4 членов (n = 4).

2. Заменяем n в формуле:
Sn = 2 * (1 - (-3)^4) / (1 - (-3))

3. Возводим -3 в 4 степень:
Sn = 2 * (1 - 81) / (1 - (-3))

4. Вычисляем внутренние скобки:
Sn = 2 * (-80) / (1 + 3)

5. Складываем числа во внутренних скобках:
Sn = -160 / 4

6. Вычисляем окончательное значение:
Sn = -40

Таким образом, сумма первых 4 членов геометрической прогрессии с первым членом 2 и знаменателем -3 равна -40.

Надеюсь, что мой ответ был понятен и помог вам! Если у вас есть еще вопросы, не стесняйтесь задавать их.