Найдите сумму 1*2^1+2*2^2+3*2^3+...+9*2^9
Другие вопросы по теме Алгебра
Популярные вопросы
- 1.) Прочитайте ряди слів. Знайдіть і назвіть узагальнювальні слова. 1....
3 - Чем занимались преимущественно арии до переселения в Индию?...
3 - почему в поэме Реквием Ахматова избрала рассказа о народной трагедии от...
1 - ответьте на вопрос: почему старший жуз вошёл в состав России? (нужно написать...
2 - Найти для цепи а) I1, I2, I3 ? для цепи b) силу тока в резисторе 12 ом...
3 - M^2*n^2+m^2+4n^2+9 =10mn...
1 - Из прямого угла вдоль его сторон побежали кошки Буся и Муся. Через 40...
1 - Смешали 125 г раствора с массовой долей щелочи (NaOH) 10 % и 425 г раствора...
1 - преобразуй выражение в многочлен. Заполни пропуски. (k4 – 7t2)3 = k –...
3 - 11.Жалғаулықсыз салалас құрмалас сөйлемді табыңыз: А) Қоңырау соғылып...
3
Объяснение:
2+8+24+64+160+384+896+2048+4608=8194
∑n*2^n
Рассмотрим функцию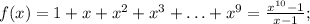
поэтому искомая сумма равна 8194.
Замечание. Мы воспользовались формулой суммы геометрической прогрессии