Найдите седьмой член прогрессии bn если b8=16 а знаменатель 3/4

Геометрическая прогрессия - это последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же, не равное нулю число (называют знаменателем геометрической прогрессии и обозначают q), т.е. bₓ = bₓ₋₁ · qˣ⁻¹ ( в учебнике буква n, но здесь в редакторе нет такой).

Поэтому:

b₈ = b₇ · q и т.к. по условию b₈ = 16, q = 3/4, то b₇ = b₈ : q, т.е.

b₇ = 16 : (3/4) = 16 · 4/3 = 64/3 = 21 целая 1/3.

ответ: 21 целая 1/3.

Объяснение:

Как известно, общий член геометрической прогрессии представляется рекуррентно по формуле

где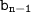 и 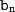- последовательные члены, а q - знаменатель прогрессии.

Так как даны b₈ и q= , то b₇ находим из рекуррентной формулы очень легко: