Найдите решение уравнения: 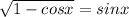
Другие вопросы по теме Алгебра
Популярные вопросы
- Чему равен объем многогранника, изображенного на рисунке?...
3 - Скільки двохцифрових чисел можна утворити з цифр 0,3,4...
2 - Скільки віршів Г.Гейне поклав на музику Роберт Шуман?...
3 - Найдите полное толкование словосочетанию крепостное право: А) Слово «рабство»...
3 - 7. Чтобы найти периметр и площадь прямоугольника, мы используем формулы P=2(a+b)...
1 - Послушать Полёт валькирий и отв. на вопросы: 1. Кто участвует в исполнении....
2 - 345. Вставь пропущенные буквы и знаки, раскрой скобки. Сделай синтак- сический...
3 - На рисунке показано направление силы, приложенной направлением движения сустава...
3 - Найдите площадь данной фигуры....
1 - ВСТАВИТЬ СЛОВА chat quality opera science media radio advertisement host interview...
1
(см. объяснение)
Объяснение:
При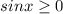 :
:
Тогда:
Уравнение решено!