Найдите решение уравнения: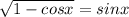
Другие вопросы по теме Алгебра
Популярные вопросы
- «Комплекс» в переводе с латинского языка означает «сплетение». Какой...
3 - «Самая старая», традиционная отрасль экономики, центральное звено...
1 - «Минусы» в работе автомобильного транспорта...
3 - «Кровеносной системой хозяйственного организма» называют отрасль...
2 - «Жунгарские ворота» связывают Казахстан с...
2 - «Казахстанской Швейцарией» называют горы...
1 - «Великие северные экспедиции», задуманные Петром 1, были проведены...
2 - Как называются карты, на которых показывают несколько взаимосвязанных...
1 - Основной причиной разнообразия рельефа на Земле является?...
2 - Какая часть населения Земли проживает на высоте менее 500 метров...
3
Первое условие:
С учётом второго условия системы, отпадает точка, которая находится на единичной окружности снизу. Окончательно: