Найдите расстояние на координатной плоскости между точками а(5; 3) и в(2; 1)​

См. приложение

Если представить на координатной плоскости 2 точки, то можно заметить прямоугольный треугольник.

Его катеты - разность соответственных координат А и В

Найдём катеты. Для этого из абсциссы А вычтем абсциссу В

5-2=3 - нижний катет треугольника

Теперь ординаты

3-(-1)=4 -  боковой катет.

По т. Пифагора легко можно найти гипотенузу, а именно она и будет расстоянием между двумя точками

S=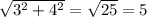 - ответ к данной задаче

При чём не важно из какой точки вычитать координаты, потому что под корнем они возводятся в квадрат. Без проблем что что-то получится отрицательное.

Итого, расстояние между двумя точками с координатами (x₁:y₁) и (x₂:y₂)