1. Алгебра
  2. Найдите производные тригонометрических

Найдите производные тригонометрических функций 17.3
a)f(x)=-cos2x+sin2x
б)f(x)=3x+cos4x
в)f(x)=x^3-2sin2x
г)f(x)=2tg2x
17.4
a)f(x)=-3ctgx-4x^3
б)f(x)=sin2x+tgx
в)f(x)=4-1/4tgx
г)f(x)=x^2ctgx
последние
P.s через photomath не получится проверял)
Если не понятно вот фото, надеюсь не проведёте!!)


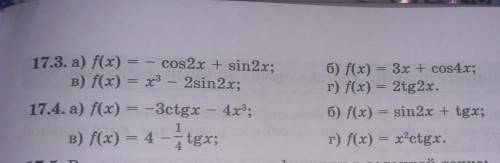
Найдите производные тригонометрических функций 17.3 a)f(x)=-cos2x+sin2x б)f(x)=3x+cos4x в)f(x)=x^3-2

Alice547 Alice547    3   08.02.2021 17:25    1

Ответы
vladajoyful vladajoyful  10.03.2021 17:26

17.3

а)

f'(x) = - ( - \sin(2x)) \times (2x)' + \cos(2x) \times (2x) '= \\ = 2 \sin(2x) + 2 \cos(2x)

б)

f'(x) = 3 - \sin(4x) \times (4x)' = 3 - 4 \sin(4x)

в)

f'(x) = 3 {x}^{2} - 2 \cos(2x) \times (2x)' = \\ = 3 {x}^{2} - 4 \cos(2x)

г)

f'(x) = \frac{2}{ { \cos }^{2} (2x)} \times (2x) '= \frac{4}{ { \cos }^{2}(2x) } \\

17.4

а)

f'(x) = - \frac{3}{ { \sin }^{2}(x) } - 12 {x}^{2} \\

б)

f'(x) = 2 \cos(2x) + \frac{1}{ { \cos}^{2} (2x)} \\

в)

f'(x) = - \frac{1}{4} \times \frac{1}{ { \cos}^{2}(x) } \\

г)

f'(x) = ( {x}^{2} )'ctgx + (ctgx)' \times {x}^{2} = \\ = 2xctgx - \frac{ {x}^{2} }{ { \sin }^{2} (x)}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
полли43 полли43  18.05.2021 11:13
(-2х)2 + 3х +5 (розклти на множники тричлен)​...
404pm 404pm  18.05.2021 11:12
Сократите дробь: 14x²b 21x* 3. ​...
yulyasmernyagi yulyasmernyagi  18.05.2021 11:11
Решить географическим уравнения -x2=-8 2x+8=x² x2=3x-2 -x²=4x...
ne1naiioo111 ne1naiioo111  08.09.2019 19:50
Решить решите систему уравнений методом сложения -2x^2-5y^2=-472 5y^2-2x^2=-312 ответы: ; -4) ; -16), (-196; 16), (196; -16), (196; 16) 3)(14; 4) ; -14), (-4; 14), (4; -14),...
dimapudov2007 dimapudov2007  08.09.2019 19:50
Соотнесите каждое выражение с множеством значений переменной, при которых оно имеет смысл. а) (a-1)(2-a)/3 б) 3/(a-1)(2-a) в) (a-1)/(2-a) 1) a≠1 2) a≠2 3) a≠1 и a≠2 4) a-любое...
HepBbI HepBbI  08.09.2019 19:50
Найдите область определения функции y=x-4/5-x...
Teroristka123 Teroristka123  08.09.2019 19:50
Найдите область определения функции y= все в корне x^2+6x+5...
1111Кристина11111 1111Кристина11111  08.09.2019 19:50
2. на сборку поступают детали с трех конвейеров. первый конвейер дает 0,3% брака; второй – 0,2%; третий – 0,4%. с первого конвейера на сборку поступило 1000 деталей; со...
lizokturina lizokturina  08.09.2019 19:50
Найдите значение выражения: 0,7ав-49+а-1,2ав+47 при а=2/3; в=9/16...
СашаМолорик СашаМолорик  08.09.2019 19:50
Периметр треугольника равен 16,2 см. две его стороны равны между собой, и каждая из них на 1,8 см больше третьей. каковы стороны треугольника? help...

Популярные вопросы