Найдите производную функции
y = -sin x + x ^ 3
Другие вопросы по теме Алгебра
Популярные вопросы
- Кто Аз по планам! Нужно составить план к мини рассказу. Лісові мишки приступають...
3 - Составить общий план 5 и 6 главы из Тарас Бульба (пунктов 10-11), и обе главы...
2 - 48. Разгадайте кроссворд «Жизнь первобытных людей»:По горизонтали: 1. ПервоеДомашнее...
1 - Ка мышка, есть - есть или любой другой.149. Составьте шуточную поэтическую или...
2 - 2. Укажите график функции y=– Х²:...
1 - 2. Найдите длину вектора с= 2a-b, если a(6; 2; 1) и (0; -1, 2)...
1 - Укажите строку, в которой перечислены только знаменательные части речи. имя...
2 - В ячейку В2 пользователь вводит день недели (например: понедельник, вторник,...
3 - Укажи три верных ответа из шести. Для растительной клетки характерно...
1 - 11,2 г мрамора растворили в избытке соляной кислоты и получили 2,24 л газа (н.у.)....
2
Відповідь: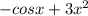
Пояснення:
Похідна суми це сума похідних, отже:
Спам'ятаємо деякі формули
Отже