Найдите производную функции в указанной точке:
а) y=x^4, x=1;
б) y=2cosx+1, x=pi/4
в) y= √x(x+2), x=4
Другие вопросы по теме Алгебра
Популярные вопросы
- Выполните действия 3x дробная черта x-4 + x+8 дробная черта x-4...
1 - Хто є засновником жанра літературної балади?...
2 - Положение горожан, феодалов...
1 - Ch3-ch-ch2-ch2-ch3+NaOH= | (йод)решите...
2 - Помагите если не знаете не пишите либо отправлю бан сор...
1 - Рассчитайте рН раствора:а) 0,200 моль/л аммиака ; б) 0,300 М азотной кислоты....
3 - 3. Оберіть пару населених пунктів України, які є містамизагальнодержавного...
1 - Докажите, что если a2 + b2 + c2 = ab + bc + ca, то a = b = c. С объяснением...
2 - Перепишите текст.Поставьте недостающие знаки препинания. 1)Кончилась большая...
2 - Серёжа на свои деньги может купить фонарик или 8 батареек к нему.Фонарик...
1
При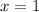 :
:
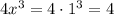 .
.
ответ:При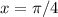 :
:
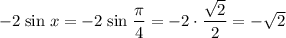 .
.
ответ:При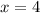 :
:
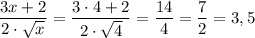 .
.
ответ: