Найдите при каких значениях параметра a функция y=-1/5cos (x/2 + pi/6) возрастает на промежутке [a-pi/6 ; a+pi/6]
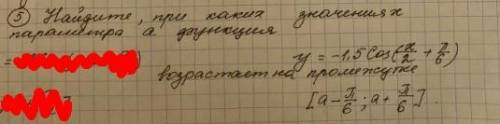
Другие вопросы по теме Алгебра
Популярные вопросы
- Напишите программу на python, которая вычисляет остаток от двух целых...
3 - Задание 2. Сопоставьте понятия и факты событий героического подвига...
2 - Здійснити перетворення//осуществить преобразования...
1 - Составьте формулы веществ по валентности: а) Zn и O б) Al и O в) Na...
2 - При горінні етану утворився вуглеводний газ об ємом 400м³ який об єм...
3 - Ы.Алтынсарин «Өнер-білім бар жұрттар» өлеңі Тыңдалымдағы автордың жастарға...
2 - Знайдiть четвертий член геометричноi прогресii (bn) якщо b1=6 q=-3...
1 - Та олзидик енбасть Кунлылыгымыс...
1 - Оцените периметр и площадь прямоугольника со сторонами а см и b см,...
1 - Напишите Неуважение к труду Филька...
2
Для начала, найдем производную данной функции. Мы можем использовать формулу производной для функций, содержащих сумму:
d/dx [cos(u(x))] = -sin(u(x)) * u'(x)
где u(x) = x/2 + pi/6. Таким образом:
y' = d/dx [(-1/5) cos(x/2 + pi/6)] = (-1/5) * -sin(x/2 + pi/6) * (1/2)
Приравняв производную к нулю, чтобы найти стационарные точки, получаем:
(-1/5) * -sin(x/2 + pi/6) * (1/2) = 0
sin(x/2 + pi/6) = 0
Теперь, воспользуемся свойствами синусовой функции, чтобы найти значения аргумента при которых sin(x/2 + pi/6) равно нулю на промежутке [a-pi/6 ; a+pi/6].
Мы знаем, что sin(x) равен нулю в точках, когда аргумент равен nπ, где n - целое число.
Таким образом, мы можем найти значения аргумента на промежутке [a-pi/6 ; a+pi/6], удовлетворяющие условию sin(x/2 + pi/6) = 0:
(a/2 + pi/6) = nπ
Решая данное уравнение относительно а, мы получаем:
a/2 = nπ - pi/6
a = 2(nπ - pi/6)
Таким образом, функция y=-1/5cos (x/2 + pi/6) возрастает на промежутке [a-pi/6 ; a+pi/6], когда параметр a принимает значения a = 2(nπ - pi/6), где n - целое число.
Например, если n = 0, то a = 2(-pi/6) = -pi/3. Если n = 1, то a = 2(π - pi/6) = 11π/6.
Надеюсь, этот ответ понятен для вас. Если у вас возникли еще вопросы или требуется дополнительное объяснение, пожалуйста, сообщите мне.