Найдите площадь фигуры, ограниченную линиями. xy=6 и x+y-7=0. только подробно.

Ответы

mihailgrand 08.10.2020 12:53

Графиком функции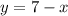 y=7-x является прямая.

Графиком функции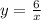 $y= \frac{6}{x}$ являются ветви гиперболы.

Найдем абсциссы точек пересечения заданных линий:

$\left \{ {{y= \frac{6}{x} } \atop {y=7-x}} \right.\\ \frac{6}{x} =7-x\\-x^2+7x-6=0\\x_1=1\\x_2=6\\$

x_1,x_2 - пределы интегрирования. (на рисунке изображены как "a" и "b".

$S= \int\limits^6_1 ({7-x- \frac{6}{x}) } \, dx= \int\limits^6_1 {7} \, dx - \int\limits^6_1 {x} \, dx- \int\limits^6_1{ \frac{6}{x} \, dx=7x\ |^6_1- \frac{x^2}{2}\ |^6_1-6ln|x|\ |^6_1\\$

=(42-7)-(18-0,5)-6*ln|6|=17,5-6*ln|6| ≈7,4 (кв. ед.)

Найдите площадь фигуры, ограниченную линиями. xy=6 и x+y-7=0. только подробно.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

айка392 19.04.2021 18:21

Знайдіть проміжки зростання і спадання функції у=10х +15...

Russia569 19.04.2021 18:21

довести що для будь яких двох натуральних чисел добуток їхньої суми та суми обернених до них чисел не менший ніж 4...

Лика1508 19.04.2021 18:22

Решите систему уровнения 5x+2у 20 мин осталось...

масяня194 19.04.2021 18:22

Розв яжіть нерівність 2(8х + 5) варианты ответа 16x – 8.XERхеохе(°/16 ;+ою)хе(0,125; + %)...

ulianaroingova 19.04.2021 18:23

вы наша последняя надежда НАГИТО...

leha2018 14.05.2020 21:50

Покажите 2 пары чисел, которые могут быть решением неравенства y...

mokeevayulichk48 14.05.2020 21:50

(2-х)^2-х(х+3) и найдите его значение при х=1/14...

dilmurod9292 14.05.2020 21:50

Сократить дробь 2а²-5а-2/а²-4...

Moon133 14.05.2020 21:50

будь ласка розпишітьДва робітники, працюючи разом, можуть виконати деяку роботу за 6 днів. За скільки днів кожен робітник самостійно зможе виконати цю роботу, якщо один з них може...

RUMBANITTA 14.05.2020 21:50

Найти производную очень нужна...

Найдите площадь фигуры, ограниченную линиями. xy=6 и x+y-7=0. только подробно.

Популярные вопросы