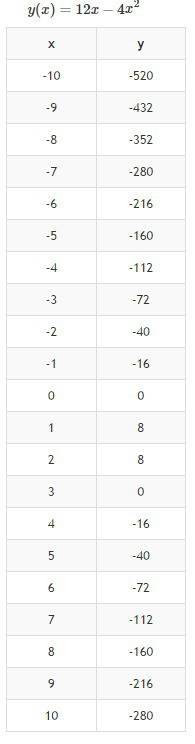
Найдите площадь фигуры, ограниченной линиями у=12х-4х₂ и у=0, предварительно сделав рисунок

Question

Алгебра: Найдите площадь фигуры, ограниченной линиями у=12х-4х₂ и у=0, предварительно сделав рисунок

Danil10031 · Answer

Чертим рисунок с учётом того, что у=0 это ось ОХ. Сразу видно о какой фигуре идёт речь и пределы интегрирования [0;3]. Функция у=12х-4х², ограничивающая фигуру, лежит выше оси ОХ, поэтому площадь:
$S= \int\limits^3_0 {(12x-4x^2)} \, dx=(6x^2- \frac{4x^3}{3} )|_0^3=6*3^2- \frac{4*3^3}{3}-0=54-36$ =18 ед²

Найдите площадь фигуры, ограниченной линиями у=12х-4х₂ и у=0, предварительно сделав рисунок

Найдите площадь фигуры, ограниченной линиями у=12х-4х₂ и у=0, предварительно сделав рисунок

Найдите площадь фигуры, ограниченной линиями у=12х-4х₂ и у=0, предварительно сделав рисунок

Популярные вопросы