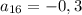Найдите первый отрицательный член арифметической прогрессии 10,2; 9,5; 8,8;
Другие вопросы по теме Алгебра
Популярные вопросы
- Запишите градусную меру угла, если его радианная мера равна7п/6...
2 - Що сприяло тому, що населення 13 колоній отримало досвід самоврядування?...
1 - Коренями якого квадратного тричлена є числа...
2 - 7.Загальною ознакою ізомерів є їх подібність/однаковість: а)фізичних...
3 - Найдите массу медного куба,сумма всех рёбер которого равна 72см.Масса...
3 - Нужна !! Наскільки глибоко вдеї просвітництва Вплинули на різн населення?...
1 - Спишите, раскрывая скобки. Расставьте недостающие знаки препинания....
1 - Облать определения функции...
2 - Решить дифференциальные уравнения первого порядке....
3 - 2 Write sentences using the words from the boxes. the dogObjecta computerthe...
1
Найдем разность арифметической прогрессии: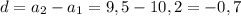
Воспользуемся формулой нахождения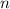 -го члена арифметической прогрессии:
-го члена арифметической прогрессии:
Найдем последний неотрицательный член данной арифметической прогрессии, решив неравенство:
Следовательно, последним неотрицательным членом данной прогрессии будет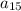 , поэтому первым отрицательным ее членом будет
, поэтому первым отрицательным ее членом будет 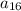 , который равен:
, который равен:
ответ: