1. Алгебра
  2. найдите первообразную (интегрирование

найдите первообразную (интегрирование по частям)
(3x + 7)cos5xdx

loveinyourhard loveinyourhard    2   02.03.2020 16:19    1

Ответы
КаМиЛлА2911 КаМиЛлА2911  11.10.2020 16:40

f(x) = (3x + 7)\cos 5x

Найдем первообразную для функции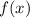 f(x) в виде неопределенного интеграла:

\displaystyle \int\limits {(3x + 7)\cos 5x} \, dx

Если подынтегральная функция может быть представлена в виде произведения двух непрерывных функций, то справедлива следующая формула:

\displaystyle \int\limits {u} \, dv = uv - \int\limits {v} \, du

Предполагается, что нахождение интеграла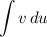 \displaystyle \int v\,du проще, чем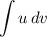 \displaystyle \int u\,dv

Таким образом, сделаем соответствующие замены:

3x + 7 = u \Rightarrow du = 3 \, dx

\cos 5x = dv \Rightarrow v = \displaystyle \int\limits {\cos 5x} \, dx = \dfrac{1}{5} \sin 5x (константу C опускаем)

Имеем:

\displaystyle \dfrac{1}{5} (3x + 7)\sin 5x - \int\limits {\dfrac{1}{5}\sin 5x \cdot 3} \, dx

Упрощаем:

\displaystyle \dfrac{1}{5} (3x + 7)\sin 5x - \dfrac{3}{5}\int\limits {\sin 5x} \, dx

\dfrac{1}{5} (3x + 7)\sin 5x + \dfrac{3}{25} \cos 5x + C

Следовательно,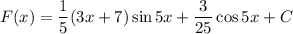 F(x) = \dfrac{1}{5} (3x + 7)\sin 5x + \dfrac{3}{25} \cos 5x + C

ответ: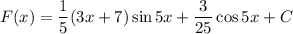 F(x) = \dfrac{1}{5} (3x + 7)\sin 5x + \dfrac{3}{25} \cos 5x + C

ПОКАЗАТЬ ОТВЕТЫ
nastya06nastik nastya06nastik  11.10.2020 16:40

Вроде как-то так

Объяснение:


найдите первообразную (интегрирование по частям) (3x + 7)cos5xdx
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
nissanbaev25 nissanbaev25  24.12.2020 15:28
Сократите дробь: x^2-4/x^2+5x+6...
hromgugd hromgugd  24.12.2020 15:29
При каких значениях х верно равенство : 25х^2 - 13х = 10х^2 + 6 ​...
rollinz14 rollinz14  24.12.2020 15:29
Кто может сделать 1? очень...
margaritamaurses margaritamaurses  24.12.2020 15:29
Составь квадратное уравнение, у которого: старший коэффициент равен 23; коэффициент при z равен 19; свободный член равен 3,37. ответ: z^2++=0...
Pwp790 Pwp790  24.12.2020 15:30
Практическая работа на построение...
spongebob2353 spongebob2353  06.05.2020 04:38
Какова вероятность, что случайно встреченный на улице человек родился 1 числа, если известно, что он родился в ноябре?...
jhdjshshdh jhdjshshdh  06.05.2020 04:41
алгебра -1*(3х-5)=5 и то что на фото...
007238 007238  06.05.2020 04:37
В одной системе координат постройте графики уравнений 2x+3y=6, 2x=6, 3y=6 и найдите координаты их точек персечения этих прямых быстрее! у меня самостоятельная работы...
ieoeoeoeosikskd ieoeoeoeosikskd  06.05.2020 04:37
Решите задачу:* Имеются прямоугольник и квадрат. Одна из сторон прямоуголь-ника равна стороне квадрата, а другая на 3 см меньше её. Из-вестно, что площадь прямоугольника на 15...
whatareyoudoing whatareyoudoing  06.05.2020 04:36
с сайтом skysmart.ru ссылка PDF...

Популярные вопросы