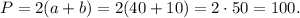Найдите периметр прямоугольника если его площадь равна 400 hа отношение соседних сторон равно 4 : 1
Другие вопросы по теме Алгебра
Популярные вопросы
- Дві прямі площини a паралельні двом прямим площини B . Чи випливає...
3 - Построить график функции y= -x квадрате(указать в каких координатных...
1 - ТЕСТ a) is b) does c) do d) was 2. My brother ___ tall and handsome....
2 - LA FAMILLE ET LES ADJECTIFS POSSESSIFS 1. Trouvez la forme féminine:...
1 - написать сочинение по географии на тему Влияние энергетики на...
2 - надо заполнить таблицу по географии. Тема: Внутреннее строение...
3 - Чем похожи и чем отличаются города...
3 - Выберете верные толкования фразеологизмов источник которых античная...
1 - Скласти і записати 4 речення з дієприкметники зворотнями з (різним...
3 - 1.Почему Запорожские казаки неоднократно просили перейти в подданство...
2
Объяснение:
Однако же решение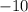 не подходит по условию задачи, так как длина стороны не может быть отрицательной. Получается, что
не подходит по условию задачи, так как длина стороны не может быть отрицательной. Получается, что 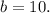
Тогда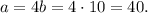
Периметр прямоугольника — удвоенная сумма смежных сторон, то есть