Найдите отношение объема конуса, описанного вокруг правильной треугольной пирамиды, к объему конуса, вписанного в эту пирамиду.

Question

Алгебра: Найдите отношение объема конуса, описанного вокруг правильной треугольной пирамиды, к объему конуса, вписанного в эту пирамиду.

Анюточка2906 · Answer

Пусть объем описанного конуса обозначени через V1, а объем вписанного через V2.

Эти конусы отличаются только радиусами оснований - окружностей описанной и вписанной в правильный треугольник - основание правильной пирамиды.

$V_1=\frac{1}{3}\pi R^2h,\ \ \ V_2=\frac{1}{3}\pi r^2h,$ где R и r - радиусы таких окружностей (оснований конусов)

Для правильного треугольника имеем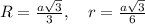 $R=\frac{a\sqrt3}{3},\ \ \ r=\frac{a\sqrt3}{6}$

Отсюда R=2r

Для описанного конуса его объем равен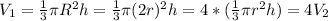 $V_1=\frac{1}{3}\pi R^2h=\frac{1}{3}\pi (2r)^2h=4*(\frac{1}{3}\pi r^2h)=4V_2$

Итак объем описанного конуса больше объема вписанного конуса в 4 раза.

ответ : отношение равно 4:1.