Найдите область значения функции:
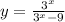
Другие вопросы по теме Алгебра
Популярные вопросы
- Үзіндіден деректі және дерексіз зат есімдерді табыңыз. Өнер-білім бар...
1 - Какие множетели есть у числа 63?...
3 - 843. 1) |2 - 1,5) = 4; 2) |3 - 2) = 5;3) 2x - 3) = 0;4) 6 -5x = 0;5) x...
1 - Перевод! желательно точный, так как переводя самой большинство слов неправильные...
1 - Верно ли равенство? (ac + 4)2 = a?c2 + 8ас + 16...
3 - Краткая запись таблицой математика 4 класс рудницкая часть 1 стр153 номер...
3 - 5-жұмыс парағы. Көлеңкені өзгертуге бола ма?...
1 - СДЕЛАЙТЕ 2 ПРИМЕРА НА ДРОБИ С ОБЬЯСНЕНИЕМ НА ×,÷,-,+....
1 - З поданого набору літер створіть і запишіть максимально можливу кількість...
1 - 60 :15 78:13, 54:18 ,98;14 как решить эти примеры?...
1
y ∈ R \ {0} или y ∈ (-∞; 0) ∪ (0; +∞).
Объяснение:
Область значения функции - множество чисел, которые может принимать функция (функция - это у). То есть это все числа, кроме y = 0.
Найдем, когда у будет равен нулю:
3ˣ = 0 - нет такого значения (так как значения показательной функции всегда положительны).
Значит, что область значений данной функции: y ∈ R \ {0} или y ∈ (-∞; 0) ∪ (0; +∞).