1. Алгебра
  2. Найдите область значений

Найдите область значений функции: y=3sin2x-4cos2x

HNLLZ HNLLZ    2   24.04.2019 16:00    2

Ответы
denvolk00 denvolk00  08.06.2020 17:51

Формула преобразования тригонометрического выражения

Acos\alpha +Bsin\beta =\sqrt{A^2+B^2} cos(\alpha-\gamma) \\ \\ A^2+B^2\neq 0

Вс аргумент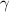 \gamma определяется из условий

cos\gamma=\dfrac{A}{\sqrt{A^2+B^2}} ;\ \ sin\gamma=\dfrac{B}{\sqrt{A^2+B^2}}

=====================================================

y = 3sin(2x)-4cos(2x);\ \ A = -4;\ \ B = 3\\ \\ \sqrt{A^2+B^2} =\sqrt{(-4)^2+3^2} =5\\ \\y = 3sin(2x)-4cos(2x)=5cos(2x-\gamma)\\ \\ -1\leq cos(2x-\gamma)\leq 1\\ \\ -5\leq 5cos(2x - \gamma)\leq 5

ответ: область значений y ∈ [-5; 5]

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
81810000 81810000  06.09.2021 17:12
Алгебра9 класс решить даю!...
школа5553 школа5553  06.09.2021 17:13
. №0.9. Применяя формулы сокращенного умножения, разложите многочлен на множители:• 1. 4x² - 9y²• 2. -25a² + b²• 3. 27x³ - y³• 4. 8a³ + b³• 5. 4m² - 4mn + n²• 6. 8xy + y² + 16x²•...
ULYA1111111 ULYA1111111  06.09.2021 17:13
-27+(-3),317+(-12) как решить...
pomogite361 pomogite361  06.09.2021 17:13
При яких значеннях х дріб 81-x² 2x+6 перетворюється на нуль?...
Kotbarsikrulit Kotbarsikrulit  06.09.2021 17:13
1) Упростить (а-b)^2+2ab2) Разложите на множители (x+y)-x^2+y^2...
1526962 1526962  06.09.2021 17:13
фотку прикрепляю. Только 1.008...
опшпищи опшпищи  06.09.2021 17:13
Розкласти на множники: 1) x³-9x2) 20-125c²;3) 2n2 + 16n+32; 4) 4m³-32c³;5) 14y³-14y....
ivankisa12 ivankisa12  06.09.2021 17:14
Приведите одночлены к стандартному виду -9y×(-2/3 xy во второй степени)...
111ВсЕзНаЙкА111 111ВсЕзНаЙкА111  06.09.2021 17:14
( ) ТЕМА ПОВТОРЕНИЕ ФОРМУЛА СОКРАЩЕННОГО УМНОЖЕНИЯ 1 (x-10)(x+10) 2 (2a+3)(2a-3) 3 (x+7)^2 4 (a-2x)^2 5 (5y-1)^2+(5y-3)(5y+3) 6 (3x+4)(3x-4)-(5x-20)^2...
Лилия3510 Лилия3510  06.09.2021 17:14
Решите, у этой фигуры найти S...

Популярные вопросы