Найдите область определения выражения корень из x2 +16x+64/x2-49

Ответы

aaaaanastya92 02.10.2020 20:03

$\dfrac{\sqrt{x^2+16x+64}}{x^2-49}=\dfrac{\sqrt{(x+8)^2}}{x^2-49}=\dfrac{|x+8|}{(x-7)(x+7)}$

Выражение существует, когда знаменатель дроби не обращается к нулю

$(x-7)(x+7)\ne 0\\ x_1\ne 7\\ x_2\ne -7$

Область определения выражения: $x \in (-\infty;-7)\cup(-7;7)\cup(7;+\infty).$

Если в условии все выражение под корнем, то...

$\sqrt{\dfrac{x^2+16x+64}{x^2-49}}=\sqrt{\dfrac{(x+8)^2}{x^2-49}}=\dfrac{|x+8|}{\sqrt{x^2-49}}$

Выражение имеет смысл, когда подкоренное выражение неотрицательно и знаменатель дроби не обращается к нулю.

$\displaystyle \left \{ {{x^2-49\geq0} \atop {x^2-49\ne 0}} \right. ~~\Rightarrow~~~ x^2-490~~\Rightarrow~~ |x|7~\Rightarrow~\left[\begin{array}{ccc}x7\\ \\ x$

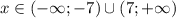При $x \in (-\infty;-7)\cup (7;+\infty)$ выражение имеет смысл

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

КлубВинксРоссия17 09.04.2020 09:12

Умножение одночлена на многочлен....

ДинаВаитова 09.04.2020 09:12

Построить в одной координатной плоскости графики функций: 1)у=3х, у=3х-2, y=3х+3. 2)у=4х+2, у=-2х+1. 3)у=5x+1, y=5x+1...

Даня1233221 09.04.2020 09:12

Какие из пар чисел (1;1) (1;2) (3;7) являются решением уравнения...

ира1288 09.04.2020 09:11

Сделать все по А1 б) это -y , еще раз сделать все задания...

ulianaroingova 16.11.2020 19:05

Докажите тождествоДробь 4/a-b + 9 /a+b - 8a/ a^2-b^2= 5/a+b...

Скрррррооо 16.11.2020 19:05

При каких значениях n уравнение 9х²-n=0 не имеет корней...

Catiy 22.06.2019 16:50

Вычислить tg40·ctg50 (40 и 50 градусов)...

allegron4567 06.09.2019 02:00

Постройте графики функций 1)y=-4x²+1; 2)y=-4/x-2; 3)y=√x-1 !...

tamirisis7sk 06.09.2019 02:00

Раскрыть скобки 1) а+(2b-3c) 2) a-(2b+3c)...

kateryna264 06.09.2019 02:00

A²=(a+1)(a-1), доказать что при любых значениях a верно это равенство...

Найдите область определения выражения корень из x2 +16x+64/x2-49

Популярные вопросы