Найдите область определения функции

Функция имеет смысл при любых вещественных значениях аргумента, при которых под корнем четной степени не стоит отрицательное число и знаменатель дроби не обращается в ноль.

Для данной функции:

1) Выражение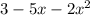 должно быть неотрицательным, как подкоренное, и не равно нулю, как квадратный корень знаменателя, т. е.

2) Выражение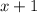 должно быть неотрицательным, как подкоренное:

Итак, мы имеем ограничения:

Решением этой системы является множество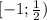 , соответственно, областью определения будет множество .

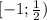ответ: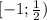 .