Найдите область определения функции 5
—————
(5-2х)•(4х+7)
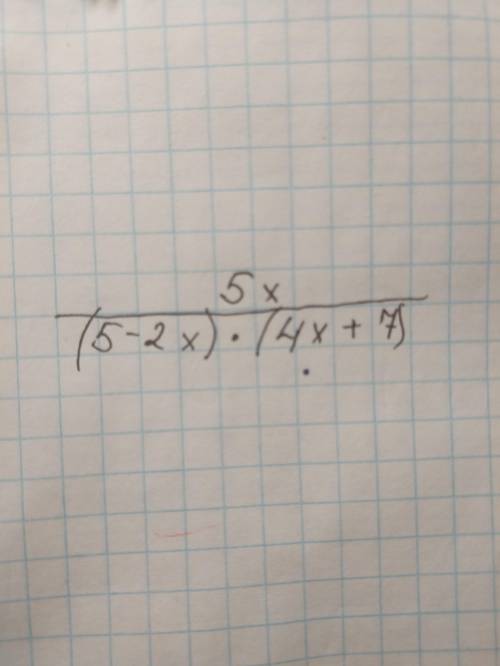
Другие вопросы по теме Алгебра
Популярные вопросы
- Какие растения занесены в красную книгу россии? а)тысячелистник обыкновенный. б)женьшень...
1 - Напишите молекулярное, полное и сокращенное ионное уравнение реакции взаимодействия...
1 - Рассмотрите особенности внешнего строения лягушки (камышовая жаба). опишите форму...
3 - Предложение со ловом оркестр и предложение со словом коллектив...
1 - Вчетырех одинаковых пакетах 12 кг помидоров. сколько килограммов помидоров в трех...
3 - Вычислить 3 sin 30+3tg45-cos 45-10сtg45 (2tg30-tg60): cos30 sin60*сos30-tg45...
2 - Отцу 45 лет .сын на 36 лет моложе отца.во сколько раз сын моложе отца?...
3 - Вкаком случае у мужчины-дальтоника может быть внук-дальтоник. только не в письменном...
2 - В19 часов от двух пристаней, расстояние между которыми 3км,одновременно в одном...
1 - Решите неравенство: 2x+7 5(2-x)+4...
1
5×4Х +5 ×7-2Х +4Х -2Х ×7
20Х +35-8 квадрат -14Х
6Х +35 -8квадрат
-8Хквадрат +6Х +35
Объяснение:
правильно у нас сегодня было это тема
В данном случае у нас имеется дробь, и функция не будет определена, когда знаменатель (в данном случае (5-2х)•(4х+7)) будет равен нулю. Это происходит потому, что деление на ноль является недопустимой операцией.
Чтобы найти область определения, нужно решить уравнение (5-2х)•(4х+7) = 0 и найти значения переменной х, при которых это равенство выполняется.
1. Решим уравнение (5-2х)•(4х+7) = 0.
Мы можем использовать метод нулевого произведения для решения этого уравнения. Согласно этому методу уравнение равно нулю, если один из множителей равен нулю.
(5-2х)•(4х+7) = 0 равносильно двум уравнениям:
5 - 2х = 0 и 4х + 7 = 0.
2. Решим первое уравнение 5 - 2х = 0:
Вычитаем 5 из обеих сторон:
-2х = -5
Делим обе стороны на -2:
х = -5/-2
Упрощаем:
х = 5/2
3. Решим второе уравнение 4х + 7 = 0:
Вычитаем 7 из обеих сторон:
4х = -7
Делим обе стороны на 4:
х = -7/4
Таким образом, мы нашли два значения переменной х, при которых знаменатель (5-2х)•(4х+7) равен нулю: х = 5/2 и х = -7/4.
Областью определения будет множество всех значений переменной х, кроме найденных значений (х ≠ 5/2 и х ≠ -7/4).
Таким образом, областью определения функции является множество всех действительных чисел, кроме 5/2 и -7/4.