Найдите область определения функции.
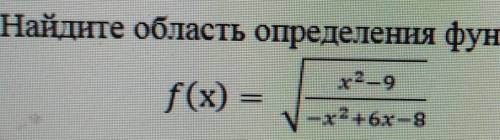
Другие вопросы по теме Алгебра
Популярные вопросы
- . Я не могу ответить на ребусы, кроме 1 и 5. Все ребусы я пронумеровала,...
2 - Возвышение Москвы: причины и хронологические рамки...
3 - Напишите оригинальное среднее по длинные сочинение на тему как...
3 - «послав на землю последний луч»- подчеркните деепричастный оборот...
3 - с математикой 5 класс номер 969...
3 - Стовпчаста діаграма розподілу хлопців 5 і дівчат 8...
3 - Какую функцию выполняет эта часть клетки? 1) запасную2) транспортную...
2 - Выбери правильные варианты ответа Какие две из приведённых ниже...
1 - Вчера когда я шла в школу было дождливое утро Дождливое утро-падеж...
1 - Яке значення має мас-медіа для дітей 14 років...
3
Нужно взять во внимание два условия.
(1) Подкоренное выражение должно быть неотрицательным.
(2) Знаменатель дроби не должен быть равен нулю.
Учитывая их, записываем следующую систему.
Для начала решим отдельно верхнее неравенство системы. Его можно решить методом интервалов, предварительно разложив на множители числитель и знаменатель.
Числитель мы разложили по формуле сокращённого умножения (разность квадратов). Для разложения знаменателя понадобится найти корни следующего уравнения:
Используя следующую формулу: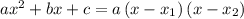 , где
, где 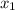 и
и 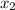 - корни уравнения
- корни уравнения 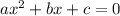 , получаем:
, получаем: 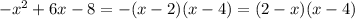 , здесь минус я занесла в первую скобку. Возвращаемся к неравенству.
, здесь минус я занесла в первую скобку. Возвращаемся к неравенству.
Решим данное неравенство методом интервалов.
Нули числителя: -3; 3.
Нули знаменателя: 2; 4.
- + - + -
----------------- -----------------о-----------------
-----------------о----------------- -----------------о-----------------> x
-----------------о-----------------> x
Так как знак в последней строке неравенства "больше или равно", то подходят те промежутки, где стоит знак "плюс". В нашем случае: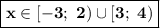 .
.
Решением нижнего выражения являются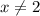 и
и 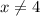 . В решении неравенства выше эти два значения и так выколоты (стоят круглые скобки), поэтому область определения таковой и остаётся.
. В решении неравенства выше эти два значения и так выколоты (стоят круглые скобки), поэтому область определения таковой и остаётся.
ответ: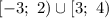 .
.