1. Алгебра
  2. Найдите область определения

Найдите область определения функции. ------------------------------------------------------------- Огромное распишите каждое действие в решении выражения, желательно через встроенную среду написания математики в знаниях. Кидать ответ с фотомача для набора - 1 звезда и жалоба. --------------------------------------------------------------


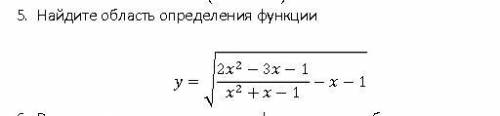
Найдите область определения функции. -------------------------------------------------------------

theaziimut theaziimut    1   20.06.2020 18:54    7

Ответы
89286163503 89286163503  15.10.2020 14:32

Первое, что можем заметить, это то, что выражение под корнем больше/равно нулю. Также замечаем, что знаменатель в дробовом выражении не может равняться нулю (Это записывать не нужно, так как будет включаться в решение неравенства).

Решим неравенство:

\frac{2x^{2}-3x-1}{x^{2}+x-1} -x-1 \geq 0\\\frac{2x^{2}-3x-1}{x^{2}+x-1} - (x+1) \geq 0\\\frac{2x^{2}-3x-1}{x^{2}+x-1} - \frac{(x+1)(x^{2}+x-1)}{x^{2}+x-1} \geq 0\\\frac{2x^{2}-3x-1-(x+1)(x^{2}+x-1)}{x^{2}+x-1} \geq 0\\\frac{2x^{2}-3x-1-(x^{3}+x^{2}-x+x^{2}+x-1}{x^{2}+x-1} \geq 0\\\frac{2x^{2}-3x-1-x^{3}-x^{2}+x-x^{2}-x+1}{x^{2}+x-1} \geq 0\\\frac{-x^{3}-3x}{x^{2}+x-1} \geq 0\\\frac{-x(x^{2}+3)}{x^{2}+x-1} \geq 0\\\frac{x(x^{2}+3)}{x^{2}+x-1} \leq 0\\

\frac{x(x^{2}+3)}{(x - \frac{-1-\sqrt{5}}{2})(x - \frac{-1+\sqrt{5}}{2})} \leq 0

Отсюда имеем решение (значит и область определения):

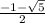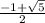x∈( -∞ ; \frac{-1-\sqrt{5}}{2} ) ∪ [ 0 ; \frac{-1+\sqrt{5}}{2} )

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
kall4 kall4  28.04.2020 15:58
решить неравенство (x-1)(x-3)(x+4) 0...
polinamalina2004 polinamalina2004  28.04.2020 15:58
Расстояние между двумя базами отдыха по реке равно 60 км. Это расстояние катер проплывает по течению реки за 2 ч., а против течения — за 3 ч. Найди собственную скорость катера и...
Dilnaz200301 Dilnaz200301  28.04.2020 15:57
Сторона квадрата равна 6 см. Вычисли диагональ квадрата....
СвятаяSaints СвятаяSaints  28.04.2020 15:57
Умоляю надо сдать до 16 00...
Тимыч08 Тимыч08  28.04.2020 15:57
ДО ТЬ (завдання) У тестах до завдання наводиться 5 відповідей , із який тільки одна правильна. Знайдіть імовірність того що навмання вибрана відповідь буде правильна...
dashamaltseva64 dashamaltseva64  28.04.2020 15:57
Реши неравенство x2+4 0​...
vikazelenaya1 vikazelenaya1  28.04.2020 15:57
Решите неравенства 1) -2х+4≥0 2) 3х-6 0 3) -2х-6≤0 4) -3х+9 0 5) 3х+1≥2х-3 6) -4х+3 -2х-1...
даша89194733164 даша89194733164  14.05.2020 23:15
Заполните пропуски. Найдите значение выражений. ответы запишите в виде десятичной дроби....
айдын23 айдын23  14.05.2020 23:15
Постройте в одной системе координат графики y=-x²+2 и y=-x укажите координаты точек пересечения этих графиков....
Файрома Файрома  14.05.2020 23:15
Биатлонист 4 раза стреляет по мишеням. Вероятность попадания при одном выстреле равна 0,5. Найдите вероятность того, что биатлонист первые 3 раза попал в мишени, а последний раз...

Популярные вопросы