найдите область определения алгебраической дроби. ответ запиши в виде числового промежутка 1) x-1/(x+3)^2 - 16 и т.д
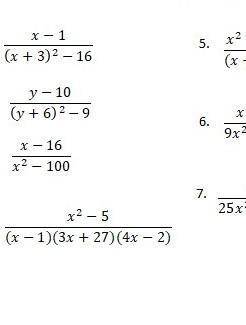
Другие вопросы по теме Алгебра
Популярные вопросы
- Паралельні прямі AB, CD i MN перетинають сторони кута з вершиною в...
2 - Наслідки христових походів для європейців...
3 - рыжие волосы рецессивный признак черные доминантные при каком браке...
2 - напряженность электрического поля в точке, где находится заряд 10-7...
2 - Известно, что отрезки BC, DE и ZX, NM по парам — пропорциональные отрезки....
3 - При каких значениях переменнвх имеет смысл выражения:A) 7/y-8 B) 4y/2y-6...
1 - Простая задача маленькая если не правильно то бан...
3 - Визначте річну кількість опадів для міста Дніпро, якщо величина випаровуваності...
2 - Укажіть органели, здатні до самовідновлення: а) рибосоми; б) хлоропласти;...
3 - Небольшое сочинение ( полcтраницы-страница) на тему: «Почему жанр сказки...
1
Для данной алгебраической дроби, знаменатель равен (x + 3)^2 - 16. Чтобы найти значения переменной, при которых он не равен нулю, мы должны решить уравнение (x + 3)^2 - 16 ≠ 0.
Начнем с раскрытия квадрата (x + 3)^2:
(x + 3)^2 = x^2 + 6x + 9
Теперь заменяем это значение в уравнении:
x^2 + 6x + 9 - 16 ≠ 0
x^2 + 6x - 7 ≠ 0
Затем, пытаемся решить уравнение на равенство нулю. Можно попробовать разложение на множители или использовать квадратное уравнение.
(x + 7)(x - 1) ≠ 0
Теперь найденные значения x, при которых выражение в знаменателе не равно нулю:
x ≠ -7 и x ≠ 1
Область определения алгебраической дроби - это все значения переменной x, за исключением -7 и 1. Мы можем записать ответ в виде числового промежутка:
(-∞, -7) U (-7, 1) U (1, +∞)
Таким образом, область определения алгебраической дроби представляет собой числовой промежуток, который включает все значения переменной x, за исключением -7 и 1.