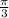Найдите наименьший положительный период функций: а) f (х) = tg (1 - 3х) б) f (x) = cos² 2x - sin² 2 x в) f (x) = 2 sin 3x cos 3x
Другие вопросы по теме Алгебра
Популярные вопросы
- Найдите угол А треугольника АВС, если: 1) АВ = 6 см, ВС = 2√6 см, АС...
1 - Две стороны треугольника равны 9 см и 21 см, а угол, противолежащий...
3 - Сторона треугольника равна 30 см, а медианы, проведённые к двум другим...
3 - В треугольнике АВС АС = 9 см, ВС = 7 см. Может ли sinА быть равным 4/5...
1 - В треугольнике ABC АВ = c, A = a, C = у. Найдите стороны ВС и АС...
3 - Диагонали параллелограмма равны 18 см и 26 см, а одна из сторон на 10...
2 - Стороны треугольника равны 8 см, 9 см и 13 см. Найдите медиану треугольника,...
2 - В треугольнике ABC провели биссектрису СЕ. Найдите стороны АС и ВС и...
3 - В треугольнике ABC C = 73 В = 77 отрезок ВМ — высота треугольника. Найдите...
2 - В равнобедренном треугольнике основание равно а, а угол при основании...
1
Наименьший положительный период функции определяется по формуле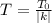 , где T₀ — период основной функции, а k — коэффициент перед x.
, где T₀ — период основной функции, а k — коэффициент перед x.
а)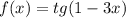
Период тангенса T₀ = π. Тогда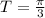
б)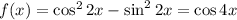
Период косинуса T₀ = 2π. Тогда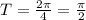
в)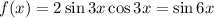
Период синуса T₀ = 2π. Тогда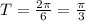
ответ: а)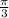 ; б)
; б) 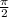 ; в)
; в)