Найдите наибольшее значение функции y=(x-27) * e в степени 28-x на отрезке [23; 40]
Ответы
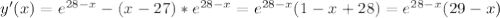
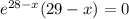 ⇒ x=29
⇒ x=29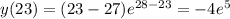
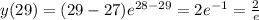 - наибольшее значение
- наибольшее значение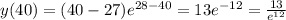
Другие вопросы по теме Алгебра
Популярные вопросы
- 1. Из суждений А И Б верно : 1) только А 2) только Б 3) и А,...
2 - помагите!Я просто не могу правда!Даю 30 б больше нет!...
2 - Решите уравнение: а) 9х^2-7х-2=0...
2 - если напишите правильно то я поставлю лучший ответ >...
3 - Сделайте синтактический разбор со схемой ШАБАШКИН, С КУРТУОЗОМ...
3 - Увеличь величины в 4 раза. 4 КГ 200 г7 КМ 300 м6 ц 23 КГ3 мб...
2 - 1. составь рассказ о произведениях Пришвина. В этом тебе вопросы:...
3 - Безопасность в сети Интернет. Урок 2 Какая клавиша используется...
3 - Составьте сложносочиненное предложение из двух простых, используя...
2 - Кто из психологов относит потребность к общению в группу соц...
1