Найдите наибольшее значение функции на отрезке [0; pi/2] y = f(x) = 12 sin x - 6√(3)x + √(3)pi + 6
![Найдите наибольшее значение функции на отрезке [0; pi/2] y = f(x) = 12 sin x - 6√(3)x + √(3)pi + 6](/tpl/images/4278/9859/40ab9.jpg)
Другие вопросы по теме Алгебра
Популярные вопросы
- Почему крестьянская реформа на руси считается не завершенной?...
2 - Поясни значення такх висловів спіймати облизня очі розбігаються летіти...
2 - Есть функция, нужно найти множину значень у=((1/2)в степени х )+ 1 !...
3 - На яку квитку схожа моя мама? сочинить текст...
3 - Как определить толщину тонкой стеклянной пластинки прямоугольной формы,имея...
3 - Сделайте полное и сокращенное ионные уравнения 2h2o+02= 2h2o...
3 - Фенологічн за тваринами іть будь ласка на сьогодні...
3 - Чем объясняется,что дистиллированная вода во всех странах обладает одними...
1 - Решить на массив из пяти элементов и подсчитать количество уникальных...
2 - Скласти. речення. за. схемами. одна пряма лінія -дві прямі. хвиляста...
1
Объяснение:
Впервую очередь найдем стационарные точки. Для нахождения мы берем производную от исходной функции и приравниваем к нулю
f(x)=12sinx-6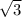 x+
x+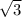 π+6
π+6
f'(x)=12cosx-6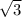
f'(x)=0
12cosx-6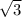 =0
=0
cosx=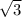 /2
/2
x=±π/6+2πk, k∈Z
итак подставляем в место k целые числа начиная с нуля для попадения в промежуток [0; π/2]
k=0;
x₁=π/6
x₂=-π/6 этот корень мы не берем так как не попадает в наш промежуток
k=1
x=π/6+2π=13π/6 уже не попадает в промежуток
значить мы нашли единственную стацианарную точку х теперь подставляем в наш начальную функцию и находим наибольшее значение.
х=π/6; fmax(π/6)=12*sin(π/6)-6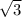 *π/6+
*π/6+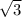 π+6=12
π+6=12