Найдите наибольшее и наименьшее значение функции 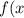 = {x}^{3} - 3x) на отрезке
на отрезке
Другие вопросы по теме Алгебра
Популярные вопросы
- Разделить по составу налетали , опоясанной...
3 - Реши уравнения.1) 14 - а = 10 2) 9 - х = 3 3) х +7=17...
3 - Уменьши каждое число на 5000 тысяч. 855000 305 100 4995000...
3 - Пример сильной личности. (такой как ник вуйчич)...
3 - Вшколе учатся 480 мальчиков и 370 девочек.сколь всего детей учатся...
1 - Может питатся как животное, и как растение в зависимости отусловий...
2 - Разобрать предложение по частям речи люди торопятся поскорей убрать...
1 - Нарисовать план местности по предмету 6 класс. и составить примерный...
2 - Покажи от каких слов и каким образованы данные слова а затем выполни...
3 - Из квадрата удвоенной суммы чисел а и b вычтите утроенную разность...
3
f(x) = x³ - 3x [0 , 2]
Найдём производную :
f'(x) = (x³)' - 3(x)' = 3x² - 3
Найдём нули производной :
3x² - 3 = 0
3(x² - 1) = 0
x² - 1 = 0
x₁ = - 1 x₂ = 1
Только x = 1 ∈ [0 ; 2]
Определим знаки производной на отрезке [0 , 2] :
- +
[0][1][2]
min
В точке x = 1 функция имеет минимум, который является наименьшим значением на заданном отрезке. Найдём это наименьшее значение :
f(1) = 1³ - 3 * 1 = 1 - 3 = - 2
Найдём значения функции на концах отрезка :
f(0) = 0³ - 3 * 0 = 0
f(2) = 2³ - 3 * 2 = 8 - 6 = 2
ответ : наименьшее значение равно - 2 , а наибольшее равно 2 .