Найдите матрицу, обратную матрице

Другие вопросы по теме Алгебра
Популярные вопросы
- Яка тема та ідея твору малишка так живуть на цій землі поети? до чого...
1 - Нужно найти аргументы для ЕГЭ по русскому в данном тексте для подтверждения...
1 - Скласти і записати повідомлення на лінгвістичну тему Відокремлені узгоджені...
2 - You …. use your credit card here. You have to pay in cash. 1) shouldn...
1 - Спишите, вставьте пропущенные буквы, обозначьте суффиксы. Кусоч..к,...
2 - Якому сьогоднішньому еквіваленту дорівнює 1$, за який умовно було придбано...
1 - Фонетична транскрипція до слів : В язка, каска, вудка, дід, рід, вогкість...
3 - Заполните таблицу:Как влияют перечисленные в таблице изменения? Расставьте...
2 - Відстань між пластинами плоского конденсатора дорівнює d=5мм , і різниця...
2 - Найрідше прийменник вживається з...
2
Имеем матрицу:
Найдем
Поскольку то существует обратная матрица
то существует обратная матрица 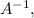 которая может быть найдена по формуле:
которая может быть найдена по формуле:
где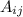 — алгебраическое дополнение элемента
— алгебраическое дополнение элемента 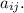
Имеем:
Проверим правильность матрицы
ответ: