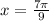Найдите корни уравнения на заданном промежутке: cos^2(3x+pi/4)-sin^2(3x+pi/4)+sqrt3/2=0 x э [3п/4; п]
Другие вопросы по теме Алгебра
Популярные вопросы
- 0,237 в обычном дробе математика ...
2 - Конгресс китапханасы такырыбына кластер жасау казак тили 4 тапсырма 179...
2 - До іть написати висновок і 5....
2 - с домашкой все видно на фото...
1 - 7. Зробити синтаксичний розбір речення.Голос його був не розкований,а,...
2 - Какими можно проверить информацию и убедиться в ее лживости? !! ...
3 - Твір роздум на тему у чому полягає краса духовного світу Мавки твір Лісова...
1 - 1. Расскажите про исторического деятеля Мурманской области и о его вкладе...
2 - Як змінюється атмосферний тиск при підніманні вгору? 2. Чому в горах атмосферний...
1 - Знайдіть довжину відрізку х на малюнку. пожайлуста ...
2
Здесь применима формула двойного угла для косинуса.
Если обозначить выражение в скобках через t, то есть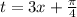 , то уравнение переписывается следующиим образом
, то уравнение переписывается следующиим образом
Воспользуемся формулой косинуса суммы углов
Заметим, что при k=6, корень уже не попадает в заданный промежуток![[\frac{3\pi}{4}; \pi]](/tpl/images/0120/4709/98547.png) ,
,
Докажем, что![\frac{7\pi}{9}\in [\frac{3\pi}{4};\pi]](/tpl/images/0120/4709/121d2.png)
То есть всего лишь один корень попадает в этот промежуток
ответ: при k=5