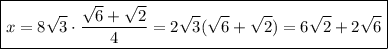найдите х и у по теореме синусов расписанно и понятно
Другие вопросы по теме Алгебра
Популярные вопросы
- нужен КРОССВОРД НА ТЕМУ ЭЛВИС ПРЕСЛИ желательно 20-30 во...
1 - Произведите полный синтаксический и пунктуационный разбор предложений,...
1 - 1. Складіть електричне коло за накресленою вами схемою. 2. Виміряйте...
3 - Необходимо составить комплекс упражнений на развитие силы спины (4-6...
2 - Доведіть,що в наслідок господарської діяльності людини в природних...
2 - Докажи, что данные сложноподчинённые предложения — с придаточным...
3 - Чим життя рабів, які перебували в привілейованому становищі, відрізняло-...
1 - Округлить число 2,04184 до десятитысячных...
1 - Выберите верные утверждения о химических свойствах водорода:в реакциях...
2 - Закат тяжело пылает на кронах деревьев, золотит их старинной позолотой....
2
Сумма внутренних углов треугольника равна 180°, значит
∠S = 180° - (∠K + ∠P) = 180° - (60° + 45°) = 75°
Согласно теореме синусов
Распишем отдельно sin 75°
Значит,