Найдите функции, обратные данным
так что первое x меньше или равно 0, а второе х больше либо равно 0

Объяснение:

Рассмотрим случай x ≤ 0

Тогда функция принимает значение

Попробуем выразить явно функцию. Для этого выделим полный квадрат в правой части:

Теперь,

Для x ≤ 0 соответствует корень, взятый с отрицательным знаком. Поэтому обратная функция (просто в полученной функции меняем местами x и y), получим:

.

Т.к. y ≤ 0, найдем соответствующее значение x:

Один кусочек нашли, займемся другим

При x ≥ 0 у нас функция принимает значение:

Выразим x через y, и после этого поменяем их местами

Т.е.

Поскольку y ≥ 0, найдем x, соответствующий этой обратной функции

Соединяя все воедино, получим следующую кусочно-заданную функцию:

1)

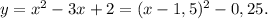
Значит, при x ≤ 1,5 (соответственно и при x < 0), функция убывает, тогда при x < 0 y > f(0) = 2.

(*): при x < 0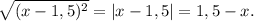

2)

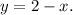
В итоге получаем: